Termodünaamika seisukoh alt kirjeldatakse gaase makroskoopiliste karakteristikute kogumiga, millest peamised on temperatuur, rõhk ja maht. Neist ühe parameetri püsivus ja ülejäänud kahe muutumine näitab, et gaasis toimub üks või teine isoprotsess. Selle artikli pühendame üksikasjalikule vastusele küsimustele, et tegemist on isohoorilise protsessiga, mille poolest see erineb isotermilistest ja isobaarilistest muutustest gaasisüsteemi olekutes.
Ideaalne gaas füüsikas

Enne kui vastate küsimusele, et tegemist on isohoorilise protsessiga, peaksite ideaalse gaasi mõistet paremini tundma õppima. Füüsikas mõistetakse selle all mistahes gaasi, mille koostises olevate osakeste keskmine kineetiline energia ületab tunduv alt nende vastasmõju potentsiaalse energia ja nende osakeste vahelised kaugused on mitu suurusjärku suuremad nende lineaarmõõtmetest. Märgitud tingimustel on teostamisel võimalikarvutused ei võta arvesse osakeste omavahelist interaktsioonienergiat (see võrdub nulliga), samuti võib eeldada, et osakesed on materiaalsed punktid, millel on teatud mass m.
Ainus protsess, mis ideaalses gaasis toimub, on osakeste kokkupõrge ainet sisaldava anuma seintega. Need kokkupõrked väljenduvad praktikas teatud rõhu olemasoluna gaasis P.
Reeglina võib praktiliste arvutuste jaoks piisava täpsusega ideaalseks gaasiks pidada igat gaasilist ainet, mis koosneb keemiliselt suhteliselt inertsetest molekulidest ning millel on madal rõhk ja kõrge temperatuur.
Ideaalset gaasi kirjeldav võrrand
Muidugi räägime Clapeyron-Mendelejevi universaalsest seadusest, mida tuleks hästi mõista, et mõista, et tegemist on isohoorilise protsessiga. Seega on universaalsel olekuvõrrandil järgmine vorm:
PV=nRT.
See tähendab, et rõhu P ja gaasimahu V korrutis võrdub absoluutse temperatuuri T ja aine koguse moolides n korrutisega, kus R on proportsionaalsustegur. Võrrandi enda kirjutas esmakordselt üles Emile Clapeyron 1834. aastal ja 19. sajandi 70. aastatel asendas D. Mendelejev selles ühe universaalse gaasikonstandi R (8,314 J/(molK) konstantsete väärtuste kogumi.)).
Vastav alt Clapeyroni-Mendelejevi võrrandile jääb suletud süsteemis gaasiosakeste arv konstantseks, seega on ainult kolm makroskoopilist parameetrit, mis võivad muutuda (T, Pja V). Viimane asjaolu on aluseks erinevate isoprotsesside mõistmisele, mida arutatakse allpool.
Mis on isohooriline protsess?
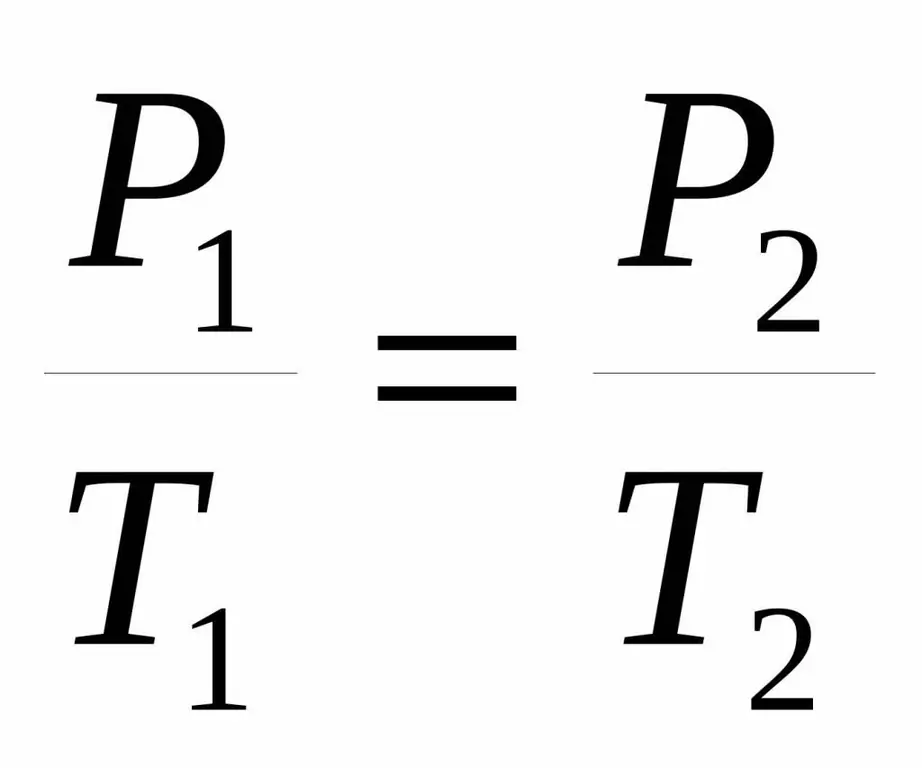
Selle protsessi all mõeldakse absoluutselt igasugust muutust süsteemi olekus, milles selle maht säilib.
Kui pöörduda universaalse olekuvõrrandi poole, võib öelda, et isohoorilises protsessis muutuvad gaasis ainult rõhk ja absoluutne temperatuur. Et täpselt mõista, kuidas termodünaamilised parameetrid muutuvad, kirjutame vastava matemaatilise avaldise:
P / T=konst.
Mõnikord antakse see võrdsus veidi erineval kujul:
P1 / T1=P2 / T 2.
Mõlemat võrdsust nimetatakse Charlesi seaduseks ühe prantsuse teadlase nime järgi, kes 18. sajandi lõpus saavutas nimetatud sõltuvuse eksperimentaalselt.

Kui koostame funktsiooni P(T) graafiku, saame sirgjoonelise sõltuvuse, mida nimetatakse isohooriks. Iga isokoor (kõikide n ja V väärtuste puhul) on sirgjoon.
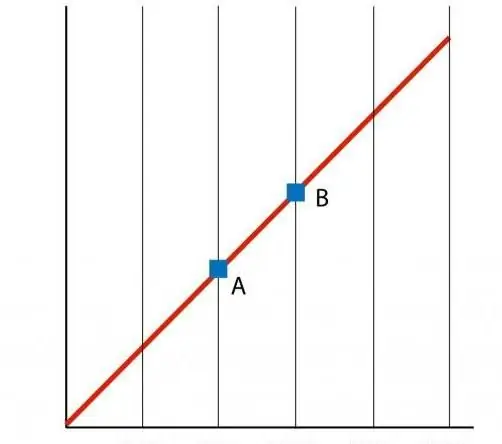
Protsessi energiakirjeldus
Nagu märgitud, on isohooriline protsess süsteemi oleku muutumine, mis toimub suletud, kuid mitte isoleeritud süsteemis. Räägime gaasi ja keskkonna vahelise soojusvahetuse võimalusest. Üldiselt annab süsteemi soojuse Q varustamine kahe tulemusega:
- muudab siseenergiat U;
- gaastöötab A, laiendades või kokkutõmbudes.
Viimane järeldus kirjutatakse matemaatiliselt järgmiselt:
Q=U + A.
Ideaalse gaasi isohooriline protsess oma määratluse järgi ei tähenda gaasi poolt tehtavat tööd, kuna selle maht jääb muutumatuks. See tähendab, et kogu süsteemile antav soojus läheb selle siseenergia suurendamiseks:
Q=U.
Kui asendame selle avaldisega siseenergia selgesõnalise valemi, saab isohoorilise protsessi soojust esitada järgmiselt:
Q=z / 2nRT.
Siin z on vabadusastmete arv, mis on määratud gaasi moodustavate molekulide polüatomilisusega. Üheaatomilise gaasi puhul z=3, kaheaatomilise gaasi puhul - 5 ning kolmeaatomilise ja enama - 6. Siin peame vabadusastmete all silmas translatsiooni- ja pöörlemisasteid.
Kui võrrelda gaasisüsteemi kütmise efektiivsust isohoorilistes ja isobaarilistes protsessides, siis esimesel juhul saame maksimaalse kasuteguri, kuna süsteemi oleku isobaarilise muutumise käigus gaas paisub ja osa soojussisendist kulub töö tegemiseks.
Isobaarne protsess
Eespool oleme üksikasjalikult kirjeldanud, et see on isohooriline protsess. Nüüd ütleme paar sõna teiste isoprotsesside kohta. Alustame isobaariga. Nimest lähtuv alt mõistetakse selle all süsteemi üleminekut olekute vahel konstantsel rõhul. Seda protsessi kirjeldab Gay-Lussaci seadus järgmiselt:
V / T=konst.
Nagu isohoori puhul, tähistab V(T) isoriba ka graafikul sirgjoont.
EestIga isobaarilise protsessi puhul on mugav arvutada gaasi tehtud tööd, kuna see võrdub konstantse rõhu ja ruumala muutuse korrutisega.
Isotermiline protsess
See on protsess, mille käigus süsteemi temperatuur jääb konstantseks. Seda kirjeldab Boyle'i-Mariotte'i seadus ideaalse gaasi jaoks. Huvitav on märkida, et see on esimene eksperimentaalselt avastatud gaasiseadus (17. sajandi teine pool). Selle matemaatiline tähistus näeb välja selline:
PV=konst.
Isohoorilised ja isotermilised protsessid erinevad oma graafilise esituse poolest, kuna funktsioon P(V) on hüperboolne, mitte lineaarne seos.
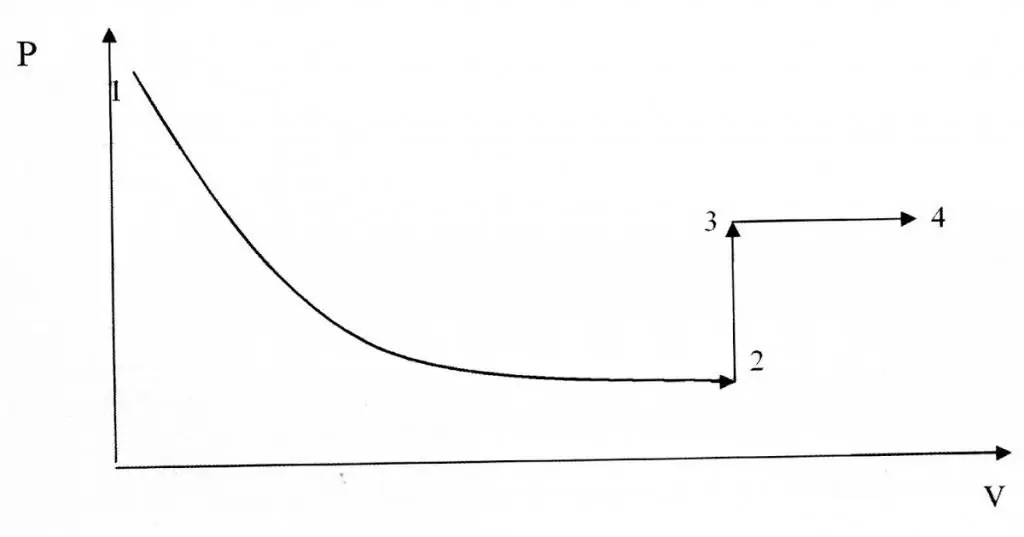
Näide probleemi lahendamisest
Konsolideerime artiklis esitatud teoreetilise teabe nende rakendusega praktilise probleemi lahendamiseks. Teadaolev alt oli puhas gaasiline lämmastik silindris rõhul 1 atmosfäär ja temperatuuril 25 °C. Pärast gaasiballooni kuumutamist ja rõhu mõõtmist selles selgus, et see oli 1,5 atmosfääri. Mis on gaasi temperatuur balloonis pärast kuumutamist? Kui palju muutus gaasi siseenergia, kui õhupallis oli 4 mooli lämmastikku.
Esimesele küsimusele vastamiseks kasutame järgmist väljendit:
P1 / T1=P2 / T 2.
Kust saame:
T2=P2 / P1 T 1.
Selles avaldises saab rõhu asendada suvaliste ühikutegamõõtmised, kuna need kahanevad ja temperatuur on ainult kelvinites. Seda öeldes saame:
T2=1,5 /1298,15=447,224 K.
Arvutatud temperatuur Celsiuse kraadides on 174 °C.
Kuna lämmastiku molekul on kaheaatomiline, saab selle siseenergia muutust kuumutamisel määrata järgmiselt:
ΔU=5/2nRΔT.
Asendades selle avaldise teadaolevad väärtused, saame vastuse ülesande teisele küsimusele: ΔU=+12,4 kJ.






