Füüsika - dünaamika - spetsiaalses osas, kui nad uurivad kehade liikumist, arvestavad nad liikuvale süsteemile mõjuvaid jõude. Viimane võib teha nii positiivset kui ka negatiivset tööd. Mõelge selles artiklis, milline on hõõrdejõu töö ja kuidas seda arvutatakse.
Töö mõiste füüsikas
Füüsikas erineb mõiste "töö" selle sõna tavalisest ideest. Töö all mõistetakse füüsikalist suurust, mis võrdub jõuvektori ja keha nihkevektori skalaarkorrutisega. Oletame, et on mingi objekt, millele jõud F¯ mõjub. Kuna sellele ei mõju ükski teine jõud, langeb selle nihkevektor l¯ suunas kokku vektoriga F¯. Nende vektorite skalaarkorrutis vastab sel juhul nende moodulite korrutisele, see on:
A=(F¯l¯)=Fl.
Väärtus A on töö, mille teeb jõud F¯ objekti liigutamiseks kauguse l võrra. Võttes arvesse väärtuste F ja l mõõtmeid, leiame, et tööd mõõdetakse SI-süsteemis njuutonites meetri kohta (Nm). Samas üksusNm-l on oma nimi - see on džaul. See tähendab, et töö mõiste on sama, mis energia mõiste. Teisisõnu, kui 1 njuutoni suurune jõud liigutab keha 1 meetri võrra, siis vastavad energiakulud on 1 džaul.
Mis on hõõrdejõud?
Hõõrdejõu töö küsimuse uurimine on võimalik, kui teate, millisest jõust me räägime. Füüsikas on hõõrdumine protsess, mis takistab ühe keha liikumist teise pinnal, kui need pinnad kokku puutuvad.
Kui arvestada ainult tahkeid kehasid, siis on nende jaoks kolme tüüpi hõõrdumist:
- puhata;
- libisemine;
- rullub.
Need jõud toimivad kokkupuutuvate pindade vahel ja on alati suunatud kehade liikumise vastu.
Puhkehõõrdumine takistab liikumist ennast, libisev hõõrdumine avaldub liikumisprotsessis, kui kehade pinnad libisevad üksteisest üle ning pinnal veereva keha ja pinna enda vahel tekib veerehõõrdumine.
Staatilise hõõrdumise näide on auto, mis on mäenõlval käsipiduril. Libmishõõrdumine avaldub siis, kui suusataja liigub lumel või uisutaja jääl. Lõpuks toimib veerehõõrdumine, kui auto ratas mööda teed liigub.
Kõigi kolme hõõrdetüübi jõud arvutatakse järgmise valemi abil:
Ft=µtN.
Siin on N tugireaktsiooni jõud, µt on hõõrdetegur. Jõud Nnäitab toe löögi suurust kehale risti pinna tasapinnaga. Mis puudutab parameetrit µt, siis seda mõõdetakse eksperimentaalselt iga hõõrdematerjali paari puhul, näiteks puit-puit, teras-lumi jne. Mõõdetud tulemused kogutakse spetsiaalsetesse tabelitesse.
Iga hõõrdejõu koefitsiendil µt on valitud materjalipaari jaoks oma väärtus. Seega on staatilise hõõrdetegur mitukümmend protsenti suurem kui libisemishõõrdetegur. Veerekoefitsient on omakorda 1-2 suurusjärku väiksem kui libisemisel.
Hõõrdejõudude töö
Nüüd, olles tutvunud töö mõistete ja hõõrdumise tüüpidega, võite minna otse artikli teema juurde. Vaatleme järjekorras igat tüüpi hõõrdejõude ja selgitame välja, millist tööd need teevad.
Alustame staatilisest hõõrdumisest. See tüüp avaldub siis, kui keha ei liigu. Kuna liikumist ei toimu, on selle nihkevektor l¯ võrdne nulliga. Viimane tähendab, et ka staatilise hõõrdejõu töö on võrdne nulliga.
Liughõõrdumine toimib definitsiooni järgi ainult siis, kui keha liigub ruumis. Kuna seda tüüpi hõõrdumise jõud on alati suunatud keha liikumise vastu, tähendab see, et see teeb negatiivset tööd. A väärtuse saab arvutada järgmise valemi abil:
A=-Ftl=-µtNl.
Libhõõrdejõu töö on suunatud keha liikumise aeglustamisele. Selle töö tulemusena muudetakse keha mehaaniline energia soojuseks.

Veerehõõrdumine, nagu libisemine, hõlmab ka keha liikumist. Veerehõõrdejõud teeb negatiivset tööd, aeglustades keha esialgset pöörlemist. Kuna me räägime keha pöörlemisest, on selle jõu töö väärtust mugav arvutada selle impulsi töö kaudu. Vastav valem kirjutatakse järgmiselt:
A=-Mθ kus M=FtR.
Siin θ on keha pöördenurk pöörlemise tulemusena, R on kaugus pinnast pöörlemisteljeni (ratta raadius).
Probleem libiseva hõõrdejõuga
Teada on, et puidust klots asub kaldpinna serval. Tasapind on kallutatud horisondi suhtes 40o nurga all. Teades, et libisemishõõrdetegur on 0,4, tasapinna pikkus on 1 meeter ja varda mass vastab 0,5 kg, on vaja leida libisemishõõrde töö.
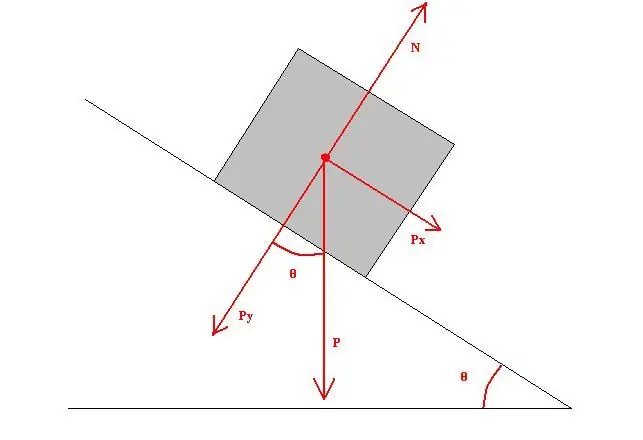
Arvutage libisemishõõrdejõud. See on võrdne:
Ft=mgcos(α)µt=0,59,81cos(40 o)0, 4=1,5 N.
Siis on vastav töö A:
A=-Ftl=-1,51=-1,5 J.
Veerehõõrdeprobleem
Teada on, et ratas veeres mingi vahemaa mööda teed ja jäi seisma. Ratta läbimõõt on 45 cm Ratta pöörete arv enne peatumist on 100. Võttes arvesse veerekoefitsienti, mis on võrdne 0,03-ga, tuleb leida, millega võrdub veerehõõrdejõu töö. Ratta mass on 5 kg.

Esm alt arvutame veerehõõrdemomendi:
M=FtR=µtmgD/2=0,0359, 81 0, 45/2=0, 331 Nm.
Kui ratta tehtud pöörete arv korrutada 2pi radiaaniga, siis saame ratta pöördenurga θ. Siis on töö valem:
A=-Mθ=-M2pin.
Kus n on pöörete arv. Asendades tingimusest momendi M ja arvu n, saame vajaliku töö: A=- 207,87 J.






