10. klassis füüsikat õppides käsitletakse dipoolide teemat. Mida see mõiste tähendab ja milliseid valemeid selle arvutamiseks kasutatakse?
Sissejuhatus
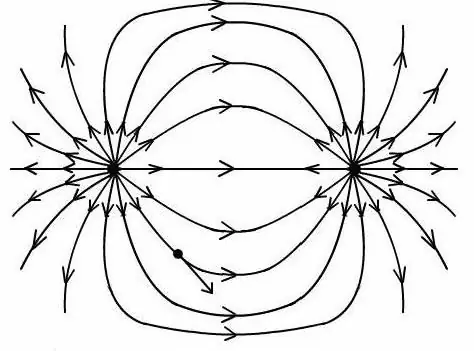
Kui asetate dipooli ühtlase elektrivälja ruumi, saate seda esitada jõujoontena. Dipool on süsteem, milles on kaks laengut, mis on parameetritelt identsed, kuid need on vastandlikud punktlaengud. Pealegi on nende vaheline kaugus palju väiksem kui dipoolvälja mis tahes punkti kaugus. Dipoolmomendi mõistet õpitakse elektrodünaamika koolikursuses (10. klass).
Dipooli telg on sirgjoon, mis läbib mõlema laengu punkte. Dipoolõlg on vektor, mis ühendab laengu ja läheb samal ajal negatiivselt laetud osakestelt positiivselt laetud osakestele. Elektrilist dipooli iseloomustab sellise oleku olemasolu nagu dipool või elektrimoment.
Dipoolmoment on definitsiooni järgi vektor, mis on arvuliselt võrdne dipoollaengu ja selle haru korrutisega. Pealegi on see koos dipooli õlaga suunatud. Jõudude summa nullvõrdsuse korral arvutame momendi väärtuse. Nurga jaoks, mis eksisteerib dipoolmomendi ja vahelelektrivälja suunalisus, iseloomulik on mehaanilise momendi olemasolu.
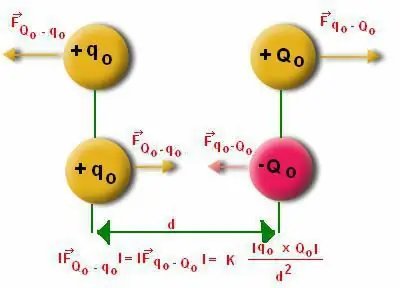
Tihti on inimestel raske dipoolstruktuurile mõjuvat moodulit arvutada. Siin on vaja arvesse võtta nurga "Alfa" arvutamise iseärasusi. Teatavasti kaldub dipool tasakaaluasendist kõrvale. Kuid dipoolmomendil endal on taastav iseloom, kuna see kipub olema liikumises.
Arvutused
Kui see dipoolmoment asetatakse ebahomogeense elektrivälja keskkonda, tekib paratamatult jõud. Sellises keskkonnas ei ole jõudude summa näitajad null. Järelikult on dipoolmomendile mõjuvad jõud, millel on punkt. Dipooli õla suurus on palju väiksem.
Valemi saab kirjutada järgmiselt: F=q (E2 - E1)=qdE, kus d on elektrivälja diferentsiaal.
Otsige uuritava füüsikalise kontseptsiooni omadusi
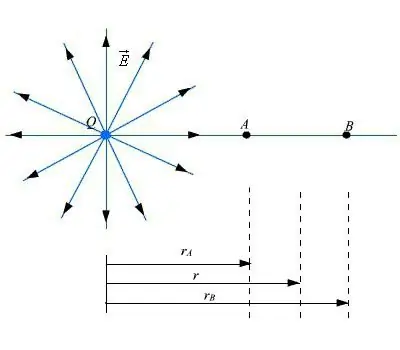
Vaatame teemat edasi. Selleks, et teha kindlaks, milline on elektrivälja tunnus, kui see luuakse laengute süsteemi abil ja lokaliseeritakse väikeses ruumis, on vaja teha mitmeid arvutusi. Näitena on toodud aatomid ja molekulid, mille koostises on elektriliselt laetud tuumad ja elektronid.
Kui on vaja otsida välja, mis on suurem kui mõõtmed, mis moodustavad osakeste asukoha, kasutame mitmeid täpseid valemeid, mis on väga keerulised. Võimalik kasutada lihtsamatligikaudsed avaldised. Oletame, et elektrivälja tekkes osalevad laengute punkthulgad qk. Need asuvad väikeses ruumis.
Välja karakteristiku arvutamiseks on lubatud ühendada kõik süsteemi laengud. Sellist süsteemi peetakse punktlaenuks Q. Suuruse indikaatorid on algses süsteemis olnud laengute summa.
Tasude asukoht
Kujutame ette, et laengu asukoht on märgitud igas kohas, kus asub tasude süsteem qk. Asukoha muutmisel, kui sellel on väikeses piirkonnas väljendatud piirangud, on selline mõju tühine, vaatepunktis väljale peaaegu märkamatu. Elektrivälja tugevuse ja potentsiaali lähendamise piirides tehakse määramised traditsiooniliste valemite abil.
Kui süsteemi kogulaengute summa on null, näivad näidatud lähenduse parameetrid umbkaudsed. See annab põhjust järeldada, et elektriväli lihts alt puudub. Kui on vaja täpsemat lähendust, koguge mõttes eraldi vaadeldava süsteemi positiivsete ja negatiivsete laengute rühmad.
Nende "keskmete" nihkumise korral teiste suhtes võib väljaparameetreid sellises süsteemis kirjeldada kui välja, millel on kaks punktlaengut, mis on suuruselt võrdsed ja märgilt vastupidised. Märgitakse, et nad on teistega võrreldes ümberasustatud. VarustamaLaengute süsteemi täpsemaks iseloomustamiseks selle lähenduse parameetrite järgi on vaja uurida dipooli omadusi elektriväljas.
Termini sissejuhatus
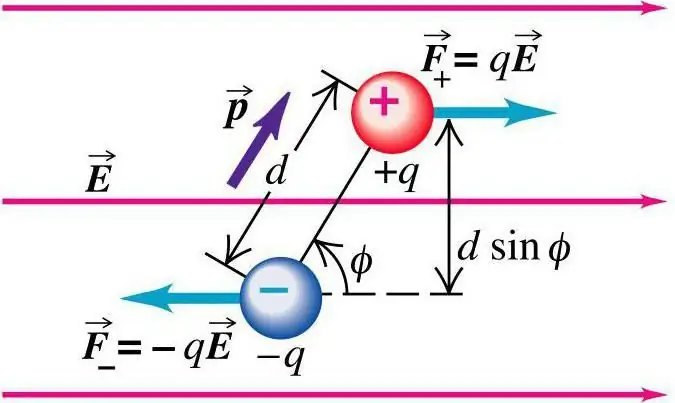
Lähme tagasi määratluse juurde. Elektriline dipool on kahe punktlaengu süsteemi määratlus. Neil on sama suurus ja vastupidised märgid. Pealegi asuvad sellised märgid teistest siltidest väikesel kaugusel.
Saate arvutada dipooli abil tekkiva protsessi karakteristiku, mis on esindatud kahe punktlaenguga: +q ja −q ning need paiknevad teiste suhtes teatud kaugusel.

Arvutuste järjekord
Alustame dipooli aksiaalpinna potentsiaali ja intensiivsuse arvutamisega. See on sirgjoon, mis jookseb kahe laengu vahel. Eeldusel, et punkt A asub dipooli keskosa suhtes kaugusel, mis on võrdne r-ga ja kui see on r >> a, on selles punktis väljapotentsiaali superpositsiooni põhimõtte kohaselt ratsionaalne kasutage avaldist elektridipooli parameetrite arvutamiseks.
Tugevuse vektori suurus arvutatakse superpositsiooni põhimõttel. Välitugevuse arvutamiseks kasutatakse potentsiaali ja väljatugevuse suhte mõistet:
Ex=−Δφ /Δx.
Sellistes tingimustes näidatakse intensiivsusvektori suunda pikisuunas dipooltelje suhtes. Selle mooduli arvutamiseks kasutatakse standardvalemit.
Tähtistäpsustused
Tuleb arvestada, et elektridipoolvälja nõrgenemine toimub kiiremini kui punktlaeng. Dipoolvälja potentsiaali vähenemine on pöördvõrdeline kauguse ruuduga ja väljatugevus on pöördvõrdeline kauguse kuubiga.
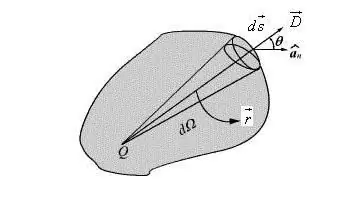
Sarnaseid, kuid kohmakamaid meetodeid kasutades leitakse dipooli potentsiaali ja väljatugevuse parameetrid suvalistest punktidest, mille asukohaparameetrid määratakse sellise arvutusmeetodi abil nagu polaarkoordinaadid: kaugus dipooli. elektridipooli keskpunkt (r) ja nurk (θ).
Arvutamine pingevektori abil
Intensiivsusvektori E mõiste on jagatud kaheks punktiks:
- Radiaal (Er), mis on suunatud sirgjoone suhtes pikisuunas.
- Selline sirgjoon ühendab määratud punkti ja dipooli keskpunkti sellega risti olevaga Eθ.
See iga komponendi lagunemine on suunatud muutuste kulgemisele, mis toimub vaadeldava punkti kõigi koordinaatidega. Leiate selle suhte järgi, mis seob väljatugevuse indikaatorid võimalike modifikatsioonidega.
Vektorkomponendi leidmisel väljatugevuse juures on oluline kindlaks teha seose olemus potentsiaalsetes muutustes, mis tekivad vaatluspunkti nihkest vektorite suunas.
Arvutage ristikomponent
Kui tehtudSelle protseduuri puhul on oluline arvestada, et suuruse avaldis väikese risti nihke korral määratakse nurga muutmisega: Δl=rΔθ. Selle väljakomponendi suurusjärgu parameetrid on võrdsed.
Pärast suhte saamist on võimalik määrata elektridipooli väli suvalises punktis, et luua pilt selle välja jõujoontega.
Oluline on arvestada, et kõik dipooli potentsiaali ja väljatugevuse määramise valemid töötavad ainult ühe dipoollaengu väärtuste ja nendevahelise kauguse korrutisega.
Dipoolne hetk
Kirjeldatud töö pealkiri on elektriliste omaduste täielik kirjeldus. Selle nimi on "süsteemi dipoolmoment".
Dipooli, mis on punktlaengute süsteem, definitsiooni järgi võib välja selgitada, et seda iseloomustab telgsümmeetria olemasolu, kui telg on sirgjoon, mis läbib mitut laengut.
Dipooli täieliku karakteristiku määramiseks märkige telje orientatsiooni suund. Arvutuste lihtsuse huvides saab määrata dipoolmomendi vektori. Selle suuruse väärtus on võrdne dipoolmomendi suurusega ja suunavektor erineb selle ja dipooli telje kokkulangevuse poolest. Seega p=qa, kui a on dipooli negatiivseid ja positiivseid laenguid ühendava vektori suund.
Sellise dipooli karakteristiku kasutamine on mugav ja võimaldab enamikul juhtudel valemit lihtsustada ja vormi andavektor. Dipoolvälja potentsiaali kirjeldus suvalise suuna punktis on kirjutatud vektori kujul.
Selliste mõistete kasutuselevõtt nagu dipoolile iseloomulik vektor ja selle dipoolmoment on teostatav lihtsustatud mudeli abil − punktlaeng ühtlases väljas, mis sisaldab laengute süsteemi, mille geomeetrilised mõõtmed ei pea arvestama, kuid oluline on teada dipoolmomenti. See on arvutuste tegemise eeltingimus.
Kuidas dipool käitub
Sellise olukorra näitel on näha dipooli käitumist. Kahe punktlaengu asukohal on üksteise suhtes fikseeritud kauguse iseloom. Need asetati ühtlase elektrivälja dipooli tingimustesse. Tegi protsessi kohta tähelepanekuid. Füüsika (elektrodünaamika) tundides käsitletakse seda kontseptsiooni üksikasjalikult. Välj alt laenguni sooritatakse jõudude mõju:
F=±qE
Need on suuruselt võrdsed ja suun alt vastupidised. Dipoolile mõjuva kogujõu näitaja on null. Kuna selline jõud avaldab mõju erinevatele punktidele, on kogumoment:
M=Fa sin a=qEa sin a=pE sin a
kus α on nurk, mis ühendab väljatugevuse vektoreid ja dipoolmomendi vektoreid. Jõumomendi olemasolu tõttu kipub süsteemi dipoolmoment pöörduma tagasi elektrivälja tugevuse vektori suundadesse.
Elektriline dipool on mõiste, mida on oluline selgelt mõista. Täpsem alt saab selle kohta lugeda internetist. Samuti võib10. klassis koolis füüsikatundides õppima, nagu eespool rääkisime.






