Meie tänase artikli teemaks on materiaalse punkti kinemaatika. Milles see on? Millised mõisted selles esinevad ja milline definitsioon tuleks sellele terminile anda? Püüame täna neile ja paljudele teistele küsimustele vastata.
Definitsioon ja mõiste
Materiaalse punkti kinemaatika pole midagi muud kui füüsika alajaotis, mida nimetatakse "mehaanikaks". Ta omakorda uurib teatud kehade liikumismustreid. Ka materiaalse punkti kinemaatika tegeleb selle probleemiga, kuid ei tee seda üldiselt. Tegelikult uurib see alajaotis meetodeid, mis võimaldavad kirjeldada kehade liikumist. Sel juhul sobivad uurimiseks vaid nn idealiseeritud kehad. Nende hulka kuuluvad: materiaalne punkt, absoluutselt jäik keha ja ideaalne gaas. Vaatleme mõisteid üksikasjalikum alt. Me kõik teame koolipingist, et materiaalseks punktiks on kombeks nimetada keha, mille mõõtmed antud olukorras võib tähelepanuta jätta. Muide, esimest korda algab materiaalse punkti translatsioonilise liikumise kinemaatikailmuvad seitsmenda klassi füüsikaõpikutes. See on kõige lihtsam haru, seega on kõige mugavam alustada selle abiga teadusega tutvumist. Omaette küsimus on, millised on materiaalse punkti kinemaatika elemendid. Neid on päris palju ja tinglikult võib need mõistmiseks jagada mitmeks erineva keerukusega tasemeks. Kui me räägime näiteks raadiusvektorist, siis põhimõtteliselt pole selle definitsioonis midagi ülemäära keerulist. Siiski nõustute, et õpilasel on sellest palju lihtsam aru saada kui kesk- või gümnaasiumiõpilasel. Ja aus alt öeldes pole vaja keskkooliõpilastele selle termini tunnuseid selgitada.
Kinemaatika loomise lühike ajalugu
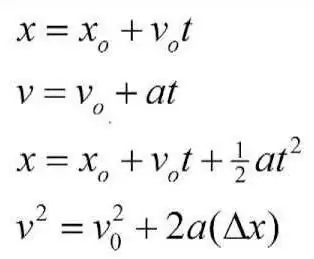
Palju, palju aastaid tagasi pühendas suur teadlane Aristoteles lõviosa oma vabast ajast füüsika kui omaette teaduse uurimisele ja kirjeldamisele. Ta tegeles ka kinemaatikaga, püüdes esitada selle põhiteesid ja mõisted, mida ühel või teisel viisil kasutatakse praktiliste ja isegi igapäevaste probleemide lahendamisel. Aristoteles andis esialgsed ideed selle kohta, millised on materiaalse punkti kinemaatika elemendid. Tema tööd ja tööd on kogu inimkonna jaoks väga väärtuslikud. Sellegipoolest tegi ta oma järeldustes märkimisväärselt palju vigu, mille põhjuseks olid teatud väärarusaamad ja valearvestused. Ühel ajal tundis Aristotelese teoste vastu huvi teine teadlane Galileo Galilei. Üks Aristotelese püstitatud põhiteesidest oli see, et keha liikuminetekib ainult siis, kui sellele mõjub mingi jõud, mille määrab intensiivsus ja suund. Galileo tõestas, et see oli viga. Jõud mõjutab liikumiskiiruse parameetrit, kuid mitte rohkem. Itaallane näitas, et jõud on kiirenduse põhjus ja see saab tekkida ainult koos sellega. Samuti pööras Galileo Galilei märkimisväärset tähelepanu vaba langemise protsessi uurimisele, tuletades sobivaid mustreid. Tõenäoliselt mäletavad kõik tema kuulsaid katseid, mille ta viis läbi Pisa tornis. Füüsik Ampère kasutas oma töödes ka kinemaatilisi lahendusi.
Algkontseptsioonid
Nagu varem mainitud, uurib kinemaatika idealiseeritud objektide liikumise kirjeldamise viise. Sel juhul saab praktikas rakendada matemaatilise analüüsi põhitõdesid, tavalist algebrat ja geomeetriat. Kuid millised mõisted (täpselt mõisted, mitte parameetriliste suuruste määratlused) on selle füüsika alajaotuse aluseks? Esiteks peaks igaüks selgelt aru saama, et materiaalse punkti translatsioonilise liikumise kinemaatika arvestab liikumist jõunäitajaid arvestamata. See tähendab, et vastavate ülesannete lahendamiseks ei vaja me jõuga seotud valemeid. Kinemaatika ei võta seda arvesse, ükskõik kui palju neid on - üks, kaks, kolm, vähem alt mitusada tuhat. Sellest hoolimata on kiirenduse olemasolu endiselt tagatud. Paljude probleemide puhul näeb materiaalse punkti liikumise kinemaatika ette kiirenduse suuruse määramise. Kuid selle nähtuse põhjused (st jõud janende olemust) ei arvestata, vaid need jäetakse välja.
Klassifikatsioon
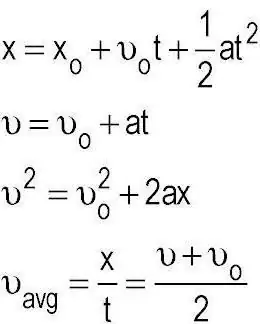
Saime teada, et kinemaatika uurib ja rakendab meetodeid kehade liikumise kirjeldamiseks, arvestamata neile mõjuvaid jõude. Muide, sellise ülesandega tegeleb teine mehaanika alajaotis, mida nimetatakse dünaamikaks. Juba seal rakenduvad Newtoni seadused, mis võimaldavad praktikas vähese teadaoleva algandmetega määrata üsna palju parameetreid. Materiaalse punkti kinemaatika põhimõisted on ruum ja aeg. Ja seoses teaduse arenguga nii üldiselt kui ka selles valdkonnas tekkis küsimus sellise kombinatsiooni kasutamise otstarbekuse kohta.
Algusest peale oli klassikaline kinemaatika. Võib öelda, et seda ei iseloomusta mitte ainult nii ajaliste kui ka ruumiliste lünkade olemasolu, vaid ka nende sõltumatus ühe või teise tugiraamistiku valikust. Muide, me räägime sellest veidi hiljem. Nüüd selgitame lihts alt, millest me räägime. Sel juhul loetakse segmenti ruumiliseks intervalliks ja ajavahemikku ajaliseks intervalliks. Kõik näib olevat selge. Seega peetakse neid lünki klassikalises kinemaatikas absoluutseks, muutumatuks, teisisõnu sõltumatuks üleminekust ühelt tugiraamistikult teisele. Kas ärirelativistlik kinemaatika. Selles võivad lüngad võrdlussüsteemide üleminekul muutuda. Veelgi õigem oleks öelda, et nad ei saa, aga ilmselt peavad. Selle tõttu on nende kahe samaaegsusjuhuslikud sündmused muutuvad samuti suhteliseks ja neile tuleb erilist tähelepanu pöörata. Seetõttu ühendatakse relativistlikus kinemaatikas kaks mõistet - ruum ja aeg - üheks.
Materiaalse punkti kinemaatika: kiirus, kiirendus ja muud suurused
Selleks, et sellest füüsika alajaost vähem alt natukenegi aru saada, on vaja orienteeruda olulisemates mõistetes, tunda definitsioone ja ette kujutada, mis on see või teine suurus üldiselt. Selles pole midagi rasket, tegelikult on kõik väga lihtne ja lihtne. Mõelge ehk alustuseks kinemaatikaülesannetes kasutatavatele põhimõistetele.
Liikumine
Mehaaniline liikumine käsitleme protsessi, mille käigus üks või teine idealiseeritud objekt muudab oma asukohta ruumis. Sel juhul võime öelda, et muutus toimub teiste kehade suhtes. Arvestada tuleb ka asjaoluga, et teatud ajaintervalli kehtestamine kahe sündmuse vahel toimub samaaegselt. Näiteks on võimalik eraldada teatud intervall, mis moodustub aja jooksul, mis kulub keha ühest asendist teise jõudmise vahel. Samuti märgime, et kehad võivad sel juhul mehaanika üldiste seaduste kohaselt üksteisega suhelda. See on just see, millega materiaalse punkti kinemaatika kõige sagedamini toimib. Võrdlussüsteem on järgmine mõiste, mis on sellega lahutamatult seotud.
Koordinaadid
Neid võib nimetada tavalisteks andmeteks, mis võimaldavad teil määrata keha asendi ühel või teisel hetkel. Koordinaadid on lahutamatult seotud nii referentssüsteemi kui ka koordinaatide ruudustikuga. Enamasti on need tähtede ja numbrite kombinatsioonid.
Raadiusvektor
Nimest peaks juba selge olema, millega tegu. Sellest hoolimata räägime sellest üksikasjalikum alt. Kui punkt liigub mööda teatud trajektoori ja me teame täpselt konkreetse referentssüsteemi algust, siis saame igal ajal joonistada raadiusvektori. See ühendab punkti algse asukoha hetke- või lõppasendiga.
Trajektoor
Seda nimetatakse pidevaks jooneks, mis rajatakse konkreetses võrdlussüsteemis materiaalse punkti liikumise tulemusena.
Kiirus (nii lineaarne kui ka nurk)
See on väärtus, mis võib öelda, kui kiiresti keha läbib teatud vahemaa intervalli.
Kiirendus (nii nurk- kui ka lineaarne)
Näitab, millise seaduse järgi ja kui intensiivselt muutub keha kiiruse parameeter.
Võib-olla siin nad on - materiaalse punkti kinemaatika põhielemendid. Tuleb märkida, et nii kiirus kui ka kiirendus on vektorsuurused. Ja see tähendab, et neil pole mitte ainult suunavat väärtust, vaid ka teatud suund. Muide, neid saab suunata nii ühes suunas kui ka vastassuunas. Esimesel juhul keha kiirendab, teisel juhul aeglustub.
Lihtsad ülesanded
Materiaalse punkti kinemaatika (kiirus, kiirendus ja vahemaa, milles on praktiliselt põhimõisted) ei hõlma mitte ainult tohutut hulka ülesandeid, vaid paljusid nende erinevaid kategooriaid. Proovime lahendada üsna lihtsa ülesande, määrates kindlaks keha läbitud vahemaa.
Oletame, et meie tingimused on järgmised. Juhi auto on stardijoonel. Operaator annab lipuga luba ja auto tõuseb järsult õhku. Tehke kindlaks, kas ta suudab võidusõitjate konkurentsis püstitada uue rekordi, kui järgmine liider läbis sajameetrise distantsi 7,8 sekundiga. Võtke auto kiirendus 3 meetrit jagatud sekundi ruuduga.
Niisiis, kuidas seda probleemi lahendada? See on üsna huvitav, kuna me ei pea teatud parameetreid "kuivatama". Seda ilmestavad käibed ja teatud olukord, mis mitmekesistab lahendamise ja näitajate otsimise protsessi. Aga millest peaksime enne ülesandele lähenemist juhinduma?
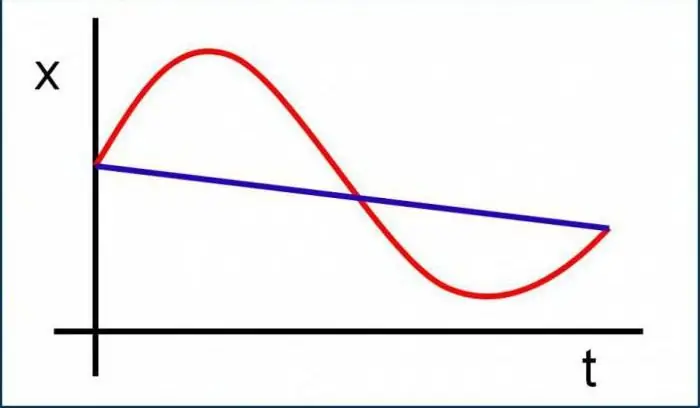
1. Materiaalse punkti kinemaatika näeb sel juhul ette kiirenduse kasutamise.
2. Lahendus eeldatakse kaugusvalemi abil, kuna selle numbriline väärtus esineb tingimustes.
Probleem on tegelikult lahendatud üsna lihts alt. Selleks võtame kauguse valemi: S=VoT + (-) AT ^ 2/2. Mis mõte sellel on? Peame välja selgitama, kui kaua rattur ettenähtud distantsi läbib, ja seejärel võrdlema seda näitajat rekordiga, et teada saada, kas ta ületab selle või mitte. Selleks eraldage aeg, saame valemitema jaoks: AT^2 + 2VoT - 2S. See pole midagi muud kui ruutvõrrand. Aga auto stardib, mis tähendab, et algkiirus on 0. Võrrandi lahendamisel võrdub diskriminant 2400. Aja leidmiseks tuleb võtta juur. Teeme seda teise kümnendkoha täpsusega: 48,98 Leidke võrrandi juur: 48,98/6=8,16 sekundit. Selgub, et juht ei suuda olemasolevat rekordit ületada.






