Nagu teate, kuulub iga füüsikaline suurus ühte kahest tüübist, see on kas skalaar või vektor. Selles artiklis käsitleme selliseid kinemaatilisi omadusi nagu kiirus ja kiirendus ning näitame ka, kuhu on suunatud kiirenduse ja kiiruse vektorid.
Mis on kiirus ja kiirendus?
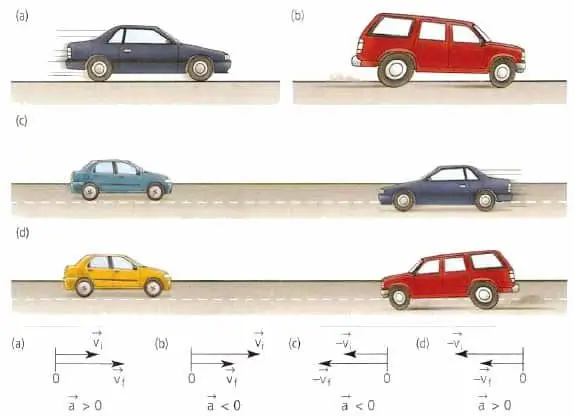
Mõlemad selles lõigus mainitud suurused on olulised mistahes liikumise tunnused, olenemata sellest, kas see liigub keha sirgjooneliselt või mööda kõverat rada.
Kiirus on koordinaatide muutumise kiirus aja jooksul. Matemaatiliselt võrdub see väärtus läbitud vahemaa aja tuletisega, see on:
v¯=dl¯/dt.
Siin on vektor l¯ suunatud tee alguspunktist lõpp-punkti.
Kiirendus on omakorda kiirus, millega kiirus ise ajas muutub. Valemi kujul saab selle kirjutada järgmiselt:
a¯=dv¯/dt.
Ilmselt võttes teise tuletisenihkevektor l¯ ajas, saame ka kiirenduse väärtuse.
Kuna kiirust mõõdetakse meetrites sekundis, mõõdetakse kiirendust vastav alt kirjalikule väljendile meetrites ruudus sekundis.

Kus on kiirenduse ja kiiruse vektorid?
Füüsikas iseloomustab keha igasugust mehaanilist liikumist tavaliselt teatud trajektoor. Viimane on mingi kujuteldav kõver, mida mööda keha ruumis liigub. Näiteks sirgjoon või ringjoon on levinumate liikumisteede peamised näited.
Keha kiirusvektor on alati suunatud liikumissuunas, olenemata sellest, kas keha aeglustab või kiirendab, kas see liigub sirgjooneliselt või mööda kurvi. Geomeetriliselt rääkides on kiirusvektor suunatud tangentsiaalselt selle trajektoori punktile, milles keha parasjagu asub.
Materiaalse või kehapunkti kiirendusvektoril pole kiirusega mingit pistmist. See vektor on suunatud kiiruse muutumise suunas. Näiteks sirgjoonelise liikumise korral võib väärtus a¯ kas suunas langeda kokku v¯-ga või olla vastupidine v¯-le.
Kehale ja kiirendusele mõjuv jõud
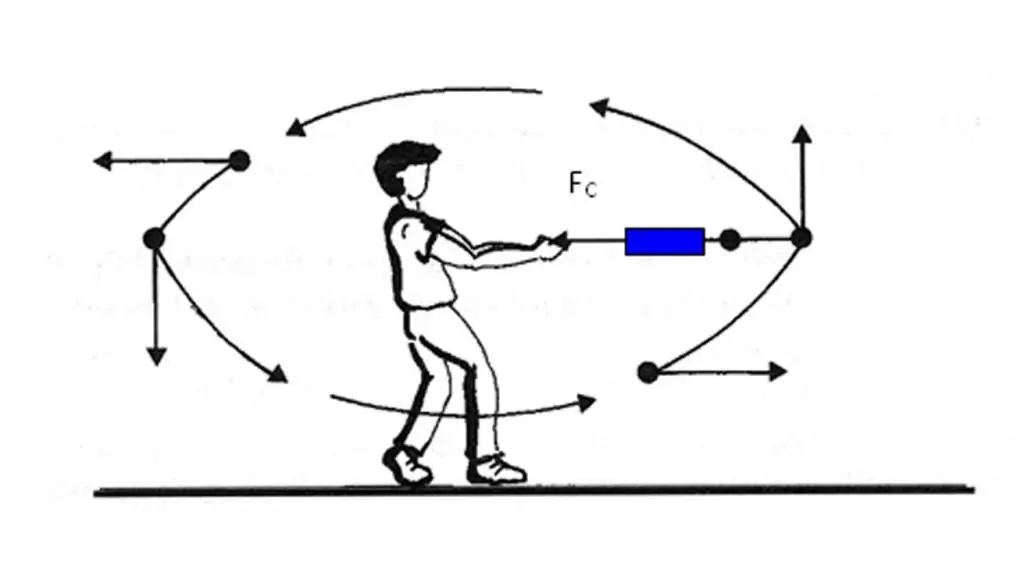
Saime teada, et keha kiirendusvektor on suunatud kiirusvektori muutumisele. Samas ei ole alati lihtne kindlaks teha, kuidas kiirus trajektoori antud punktis muutub. Veelgi enam, kiiruse muutuse määramiseks on vaja teha operatsioonvektorite erinevused. Et vältida neid raskusi vektori a¯ suuna määramisel, on kiireks teadasaamiseks veel üks viis.
Allpool on Newtoni kuulus ja kõigile üliõpilastele hästi tuntud seadus:
F¯=ma¯.
Valem näitab, et kehade kiirenduse põhjuseks on neile mõjuv jõud. Kuna mass m on skalaar, on jõuvektor F¯ ja kiirendusvektor a¯ samas suunas. Seda asjaolu tuleks meeles pidada ja praktikas rakendada, kui on vaja kindlaks määrata koguse a¯ suund.
Kui kehale mõjub mitu erinevat jõudu, siis on kiirendusvektori suund võrdne kõigi jõudude tulemuseks oleva vektoriga.
Ringliikumine ja kiirendus
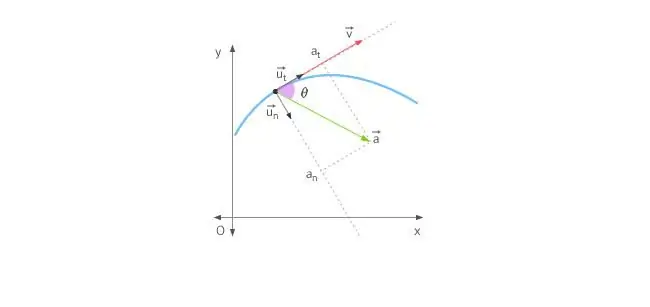
Kui keha liigub sirgjooneliselt, on kiirendus suunatud kas ette või taha. Ringjoones liikumise korral muudab olukorra keeruliseks asjaolu, et kiirusvektor muudab pidev alt oma suunda. Eespool öeldut silmas pidades määravad kogukiirenduse selle kaks komponenti: tangentsiaalne ja normaalkiirendus.
Tangsiaalne kiirendus on suunatud täpselt samamoodi kui kiiruse vektor või selle vastu. Teisisõnu, see kiirenduse komponent on suunatud piki trajektoori puutujat. Tangentsiaalne kiirendus kirjeldab kiiruse enda mooduli muutust.
Normaalkiirendus on suunatud piki normaaljoont trajektoori etteantud punktini, arvestades selle kõverust. Ringliikumise korral näitab selle komponendi vektorkeskmesse, st normaalne kiirendus on suunatud piki pöörlemisraadiust. Seda komponenti nimetatakse sageli tsentripetaalseks.
Täiskiirendus on nende komponentide summa, nii et selle vektorit saab ringjoone suhtes meelevaldselt suunata.
Kui keha pöörleb joonkiirust muutmata, siis on ainult nullist erinev normaalkomponent, seega on täiskiirenduse vektor suunatud ringi keskpunkti poole. Pange tähele, et seda keskpunkti mõjutab ka jõud, mis hoiab keha oma trajektooril. Näiteks hoiab Päikese gravitatsioonijõud meie Maad ja teisi planeete oma orbiitidel.






