Peer-retsenseerimisel, näiteks toodete konkurentsivõime hindamisel, on nagu iga teadustöö puhul vaja läbi viia statistiline andmetöötlus. Viimane algab ekspertarvamuste kooskõla määramisega, mille numbriline avaldis on vastavuskordaja.
Miks on vaja ekspertide konsensushinnangut?
See hinnang on vajalik ennekõike seetõttu, et ekspertide arvamused võivad hinnanguliste parameetrite osas suuresti erineda. Esialgu viiakse hindamine läbi näitajate järjestamise ja neile teatud olulisuse koefitsiendi (kaalu) määramise teel. Ebajärjekindel järjestus toob kaasa selle, et need koefitsiendid on statistiliselt ebausaldusväärsed. Ekspertide arvamused nende vajaliku arvuga (üle 7-10) tuleks levitada vastav alt tavaseadusele.
Kohtuvuskordaja mõiste
Nii. Järjepidevus on kooskõla. Koefitsient on mõõtmeteta suurus, mis näitab dispersiooni ja maksimaalse dispersiooni suhet üldjuhul. Üldistame need mõisted.
Konkordantsi koefitsient on arv vahemikus 0 kuni 1, mis näitab ekspertide arvamuste järjepidevust, kuimõne omaduse järjestamine. Mida lähemal see väärtus on 0-le, seda väiksemaks peetakse konsistentsi. Kui selle koefitsiendi väärtus on väiksem kui 0,3, peetakse ekspertide arvamusi vastuoluliseks. Kui koefitsiendi väärtus on vahemikus 0,3 kuni 0,7, loetakse konsistents keskmiseks. Väärtust, mis on suurem kui 0,7, peetakse suureks konsistentsiks.
Kasutusjuhud
Statistilise uurimistöö tegemisel võib tekkida olukordi, kus objekti saab iseloomustada mitte kahe jadaga, mida statistiliselt töödeldakse vastavuskordaja abil, vaid mitme jadaga, mille järjestavad vastav alt sama tasemega eksperdid. professionaalsus teatud valdkonnas.
Ekspertide poolt läbi viidud pingerea järjepidevus tuleb kindlaks teha, et kinnitada hüpoteesi õigsust, et eksperdid teevad suhteliselt täpseid mõõtmisi, mis võimaldab ekspertrühmades moodustada erinevaid rühmitusi, mis on suuresti määratud inimteguritega, eelkõige erinevused vaadetes, kontseptsioonides, erinevatest teaduslikest koolkondadest, kutsetegevuse olemusest jne.
Aste meetodi lühikirjeldus. Selle eelised ja puudused
Edastamisel kasutatakse järjestusmeetodit. Selle olemus seisneb selles, et igale objekti omadusele omistatakse oma kindel auaste. Lisaks määratakse igale ekspertrühma kuuluvale eksperdile see auastesõltumatult, mille tulemuseks on vajadus neid andmeid töödelda, et teha kindlaks ekspertarvamuste järjepidevus. See protsess viiakse läbi vastavuskoefitsiendi arvutamise teel.
Aste meetodi peamine eelis on selle rakendamise lihtsus.
Meetodi peamised puudused on järgmised:
- väike arv järjestusobjekte, kuna kui nende arv ületab 15-20, muutub objektiivsete edetabelipunktide määramine keeruliseks;
- Selle meetodi kasutamise põhjal jääb lahtiseks küsimus, kui kaugel on uuritud objektid üksteisest tähtsuselt.
Selle meetodi kasutamisel tuleb arvestada, et hinnangud põhinevad mingisugusel tõenäosusmudelil, mistõttu tuleb neid kohaldada ettevaatusega, arvestades ulatust.
Kendalli vastavuse astme koefitsient
Kasutatakse homogeenseid objekte iseloomustavate kvantitatiivsete ja kvalitatiivsete tunnuste vahelise seose määramiseks ning järjestatakse sama põhimõtte järgi.
See koefitsient määratakse järgmise valemiga:
t=2S/(n(n-1)), kus
S - teise tunnuse jadade arvu ja inversioonide arvu erinevuste summa;
n - vaatluste arv.

Arvutusalgoritm:
- X väärtused on järjestatud kasvavas või kahanevas järjekorras.
- Y-väärtused on paigutatud järjekorras, milles need vastavad x-väärtustele.
- Iga järjestikuse y järgu puhul määrake, kui palju kõrgemaid väärtusi sellele järgnevad. Need liidetakse ja arvutatakse x ja y järjestuste vastavuse mõõt.
- Samamoodi arvutatakse väiksemate väärtustega y ridade arv, mis samuti liidetakse.
- Lisage kõrgemate väärtustega auastmete arv ja madalamate väärtustega auastmete arv, mille tulemuseks on väärtus S.
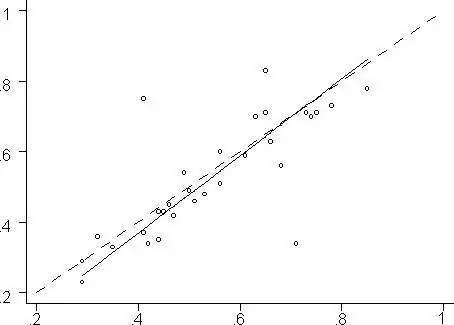
See koefitsient näitab seost kahe muutuja vahel ja enamikul juhtudel nimetatakse seda Kendalli astme korrelatsioonikordajaks. Sellist sõltuvust saab esitada graafiliselt.
Koefitsiendi määramine
Kuidas seda tehakse? Kui järjestatud tunnuste või tegurite arv ületab 2, kasutatakse vastavuskoefitsienti, mis sisuliselt on järjestuse korrelatsiooni mitmekordne variant.
Olge ettevaatlik. Vastavuskordaja arvutamine põhineb auastmete ruutude summa hälbe suhtel auastmete keskmisest ruutude summast, korrutatuna 12-ga, ekspertide ruutu, mis on korrutatud arvu kuubi vahega. objektidest ja objektide arvust.
Arvutusalgoritm
Selleks, et mõista, kust arvutusvalemi lugejas arv 12 pärineb, vaatame määramisalgoritmi.
Iga kindla eksperdi auastmetega rea kohta arvutatakse auastmete summa, mis on juhuslik väärtus.
Koordinatsioonikordaja määratletakse üldiselt dispersioonihinnangu (D) ja dispersioonihinnangu maksimaalse väärtuse suhtena(Dmax). Sõnastagem järjestikku nende suuruste definitsioonid.
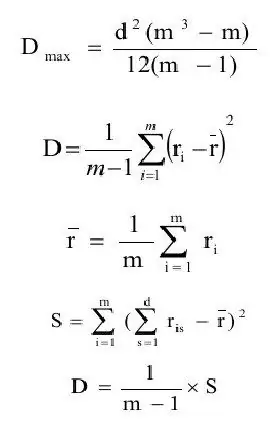
kus rkeskm. - eeldatav prognoos;
m - objektide arv.
Asendades saadud valemid D suhtes D-gamax, saame vastavuskordaja lõpliku valemi:
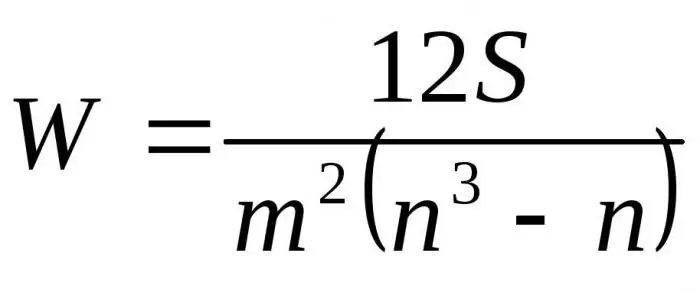
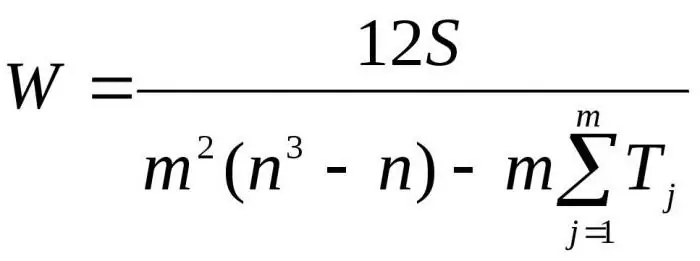
Siin m on ekspertide arv, n on objektide arv.
Esimest valemit kasutatakse vastavusteguri määramiseks, kui seotud auastmeid pole. Teist valemit kasutatakse seotud auastmete olemasolul.
Seega, vastavuskordaja arvutamine on lõppenud. Mis järgmiseks? Saadud väärtuse olulisust hinnatakse Pearsoni koefitsiendi abil, korrutades selle koefitsiendi ekspertide arvu ja vabadusastmete arvuga (m-1). Saadud kriteeriumi võrreldakse tabeli väärtusega ja kui esimese väärtus ületab viimast, räägivad nad uuritava koefitsiendi olulisusest.
Seotud auastmete puhul muutub Pearsoni kriteeriumi arvutamine mõnevõrra keerulisemaks ja seda tehakse järgmise suhtega: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Näide
Eeldame, et ekspertmeetod hindab jaemüügivõrgus müüdava või konkurentsivõimet. Toome näite vastavuskordaja arvutamisest. Enne konkurentsivõime hindamist tuleb tarbijad järjestadaselle toote hindamisse kaasatud omadused. Oletame, et need omadused on järgmised: maitse ja lõhn, konsistents ja välimus, värvus, pakend ja märgistus, rasvasisaldus, kaubanimi, tootja, hind.
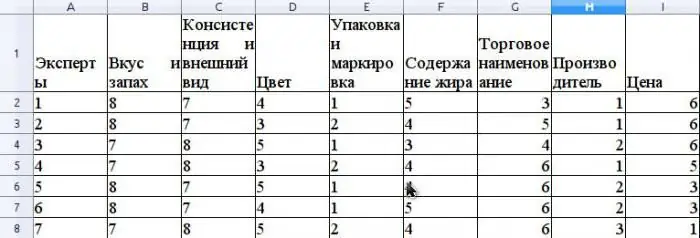
Oletame, et ekspertrühm koosneb 7 eksperdist. Joonisel on näidatud nende omaduste järjestamise tulemused.
R-i keskmine väärtus arvutatakse aritmeetilise keskmisena ja see on 31,5. S leidmiseks liidage valemi järgi erinevused ris ja r keskmise vahel. ja määrake, et S väärtus on 1718.
Arvutage kooskõlakordaja valemiga ilma seotud auastmeid kasutamata (järgud oleksid omavahel seotud, kui samal eksperdinõustajal oleks erinevate omaduste jaoks samad auastmed).
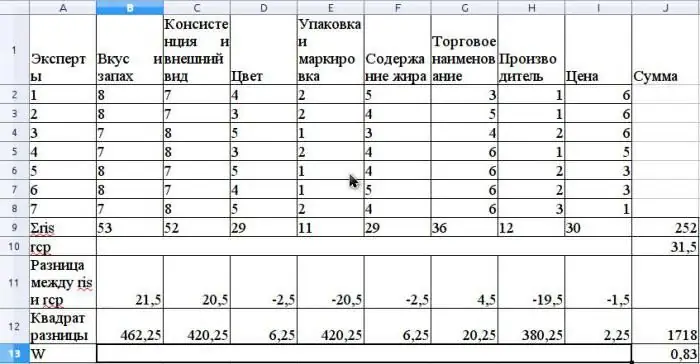
Selle koefitsiendi väärtus on 0,83. See näitab ekspertide tugevat üksmeelt.
Kontrollige selle olulisust Pearsoni testi abil:
7 x 0,83 x (8-1)=40,7.
Pearsoni tabelitest 1% olulisuse tasemel on 18,5 ja 5% - 14,1..
Näide demonstreerib arvutamise lihtsust ja ligipääsetavust iga inimese jaoks, kes tunneb matemaatiliste arvutuste põhitõdesid. Nende leevendamiseks,kasutage arvutustabeli vorme.
Kokkuvõtteks
Seega näitab vastavuskoefitsient mitmete ekspertide arvamuste kooskõla. Mida kaugemal see on 0-st ja lähemal 1-le, seda järjekindlamad on arvamused. Neid koefitsiente tuleb kinnitada Pearsoni kriteeriumi arvutamisega.






