Selleks, et oleks võimalik kujutada paberil objekte, mis tegelikkuses ei ole väga “mugavate” suurustega, mõtlesid inimesed välja skaala. Tegelikult selgitab see, mille jaoks skaala on mõeldud.
Kui kooli õppekava hakkab paljastama skaala mõistet
Esimest korda puutuvad lapsed selle sõnaga kokku piirkonna kaarte ja plaane uurides. Õpetaja selgitab, miks skaalat vaja on, mida see näitab, kasutades näitena atlaseid. Selgitatakse, et iga geograafiline objekt on nii suur, et seda oleks raske ja ebamugav täissuuruses kujutada.
Inimesed joonistasid maastiku vähendatud kujul, kuid selleks ei kasutatud täpseid suhet. Nüüd tehakse seda nutikam alt - iga kaardil kujutatud kriips ja joon on oma suuruse, mille saab korrutada kindla arvuga ning teada saada tegelik pikkus ja laius.
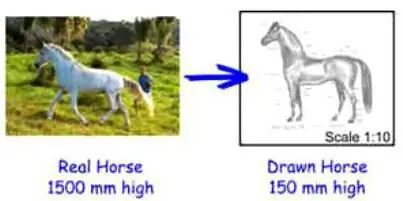
Rekordi skaala: esimene viis lugemiseks
Skaalat tähistatakse kahe kooloniga eraldatud numbriga. Esimene number tähistab mõõtmeühikuid joonisel, teinenäitab, mitu reaalühikut joonisel vastab esimesele numbrile. Näiteks kui mõnel plaanil on märgitud mõõtkava 1:1000 ja mõõtmete ühikud on märgitud sentimeetrites, siis joonisel vastab üks sentimeeter tegelikkuses 1000 cm-le. Mille jaoks siis skaala on? Selle abiga saate mitte ainult graafilise plaani teatud objekte vähendada, vaid ka nende tegelikku suurust täpselt arvutada.
Teine viis skaala salvestamiseks: mis on mugav?
Eelmist meetodit skaala kooloni kaudu kirjutamiseks nimetatakse numbriliseks. Kuid on ka nimeline skaala. Tema rekord on järgmine: 1 cm - 20 km. Selgub, et nii on võimalik kompaktselt üles kirjutada tohutud mastaabid, mida mitme nulliga numbritega ei väljendata, kui on tekkinud olukord, kus ühes sentimeetris on vaja märkida mitusada kilomeetrit. Samas on kohe selge, kui palju, mida ja milles. See salvestus on intuitiivsem ja selgem.
Skaleerimine joonistamisel: mis täiendab varem uuritud kontseptsiooni
Skaala mõistet ei kohta mitte ainult geograafias, vaid ka sellise õppeaine nagu joonistamine õppimisel. Erinevate objektide kujutamisel kasutatakse samu põhimõtteid. Kuid on oluline erinevus: siin avardab mõistet, mille jaoks mõõtkava on mõeldud, ka see, et sellega saab kujutada pisidetaile suuremas plaanis. Geograafias me sellest ei räägi, sest geograafias pole nii väikseid objekte, et neid oleks vaja suurendada. Mandrid ja mäed, jõed ja järved on igal juhul suuremad kui A4 paberilehed või isegiA1.
Joonist õppides saate kasutada skaalat, et kujutada suuremal kujul väikseid detaile, nagu polt või hammasratas.
Niisiis, miks me vajame sel juhul kaalu? Selle abiga saate väikese elemendi mugavam alt, selgem alt ja üksikasjalikum alt kujutada. Sel juhul toimub tähistus vastupidine: esimene arv on suurem kui teine ja märge 100:1 kõlab umbes nii: 100 pildi meetrilist ühikut vastab ühele tegeliku suuruse ühikule.
Mõned selgitavad näited
Mille jaoks on mõõtkava, mida see näitab väiksema objekti kujutise puhul, mis on paberil tulemus? Jällegi on meil detaili kujutise ja tegeliku objekti mõõtmete täpne suhe. Tuletage meelde sama mõõtkava 100:1. Selgub, et joonisel on sajas millimeetris tegelik suurus vaid üks millimeeter. Kui pildil on detaili laius 500 millimeetrit, on selle tegelik laius vaid 5 millimeetrit.
Kui meenutada esimest juhtumit, siis suure objekti väiksema koopia lehel olev pilt, mõõtkava 1:100, tähendab, et pildi üks millimeeter sisaldab 100 millimeetrit tegelikust suurusest. Seega, kui objekt on joonisel või kaardil 80 millimeetrit pikk, on objekti tegelik pikkus 8000 millimeetrit. Selge näide sellest, mille jaoks on mõõtkava ja milline on inimkonna mugav leiutis.
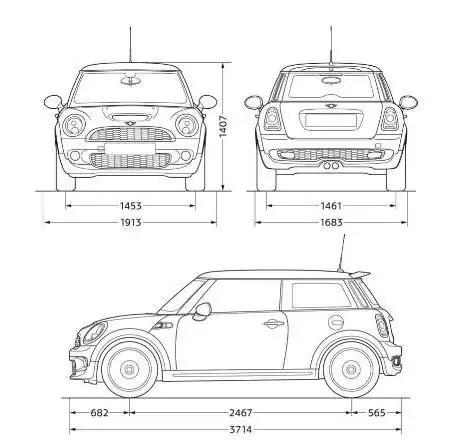
Skaala kasutamisel on peamine kohepidage meeles, et esimene number viitab pildile ja teine objektide tegelikule suurusele. Et edaspidi mitte segadusse sattuda, toimuvad nende aluste kinnistamiseks koolides praktilised geograafiatunnid, et lapsed selgitaksid ja arvutaksid atlase abil mitu korda reaalsete objektide suurusi. Sama juhtub joonistustundides.
Tee kokkuvõte
Mille jaoks skaala on? Vastus sellele küsimusele koosneb kolmest punktist, mida peate lihts alt meeles pidama:
- Esiteks - skaala on vajalik suurte objektide kuvamiseks pinnal, mis on vaatamiseks mugav.
- Teiseks - mõõtkava on vajalik väikeste objektide suuremas suuruses kujutamiseks.
- Kolmandaks - skaalat on vaja selleks, et oleks võimalik täpselt määrata reaalse objekti suurus, olenemata selle algsest suurusest, olgu see väike või suur.






