Iga koolilaps teab, et valgus homogeenses läbipaistvas keskkonnas liigub mööda sirget rada. See asjaolu võimaldab meil valguskiire mõiste raames käsitleda paljusid optilisi nähtusi. See artikkel räägib kiire langemisnurgast ja sellest, miks on oluline seda nurka teada.
Valguskiir on mikromeetriline elektromagnetlaine
Füüsikas on erineva iseloomuga laineid: heli-, mere-, elektromagnetlaineid ja mõned teised. Mõiste "kiir" kehtib aga ainult elektromagnetlainete kohta, mille osaks on nähtav spekter. Sõna "kiir" võib kujutada sirgjoonena, mis ühendab kahte ruumipunkti.
Valgust (lainena) võib vaadelda sirgjoonena, sest iga laine viitab vibratsiooni olemasolule. Vastus sellele küsimusele peitub lainepikkuse väärtuses. Niisiis ulatub mere- ja helide pikkus mõnest sentimeetrist kümnete meetriteni. Muidugi ei saa selliseid võnkumisi talaks nimetada. Valguse lainepikkus on alla ühe mikromeetri. Inimsilm ei suuda selliseid vibratsioone eristada, seetõttu tundub meile niiet näeme otsest kiirt.
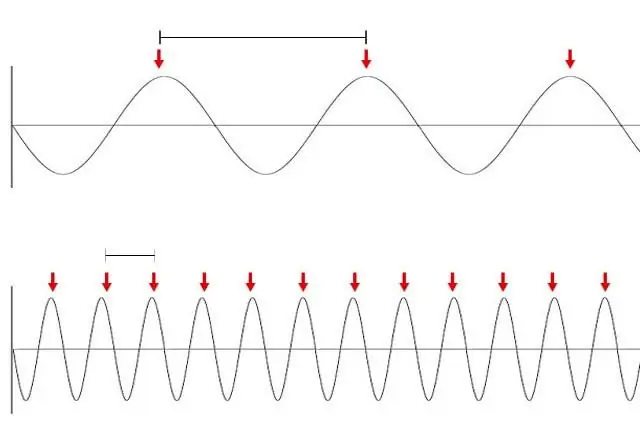
Täielikkuse huvides tuleb märkida, et valguskiir on nähtav ainult siis, kui see hakkab hajuma väikestele osakestele, näiteks tolmuses ruumis või udupiiskades.
Kus on oluline teada, millise nurga all kiir tabab takistust?
Peegelduse ja murdumise nähtused on kõige kuulsamad optilised efektid, millega inimene sõna otseses mõttes iga päev kokku puutub, kui ta vaatab end peeglist või joob pärast selles oleva lusika vaatamist klaasi teed.
Murdumise ja peegelduse matemaatiline kirjeldus nõuab teadmisi kiire langemisnurga kohta. Näiteks peegeldusnähtust iseloomustab peegeldusnurga ja langemisnurga võrdsus. Kui kirjeldada murdumisprotsessi kõrv alt, on langemisnurk ja murdumisnurk omavahel seotud siinuste funktsioonide ja keskkonna murdumisnäitajate kaudu (Snelli seadus).

Nurk, mille all valguskiir langeb kahe läbipaistva kandja vahelisele liidesele, mängib olulist rolli, kui arvestada sisemise täieliku peegelduse mõju optiliselt tihedamas materjalis. Seda efekti täheldatakse ainult langemisnurkade korral, mis on suuremad kui mõni kriitiline väärtus.
Vaatatava nurga geomeetriline määratlus
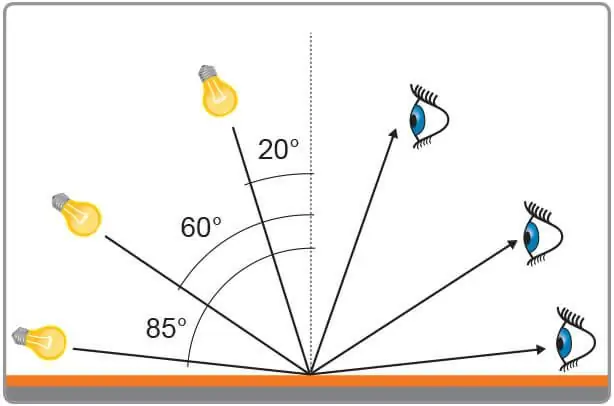
Võib eeldada, et kaht keskkonda eraldab mingi pind. See pind võib olla tasane, nagu peegli puhul, või see võib olla keerulisem, näiteks mereharjaline pind. Kujutage ette, et sellele pinnale kukubvalguskiir. Kuidas määrata valguse langemisnurka? Selle tegemine on üsna lihtne. Järgmine on toimingute jada, mida tuleks soovitud nurga leidmiseks teha.
- Esiteks peate määrama kiire ja pinna lõikepunkti.
- Läbi O tuleks joonistada vaadeldava pinnaga risti. Seda nimetatakse sageli normaalseks.
- Kiire langemisnurk on võrdne selle ja normaalnurga vahelise nurgaga. Seda saab mõõta lihtsa kraadiklaasiga.
Nagu näete, pole vaadeldava nurga leidmine keeruline. Tihti teevad õpilased aga vea, mõõtes seda tasapinna ja tala vahel. Tuleb meeles pidada, et langemisnurka mõõdetakse alati normaalsest, olenemata pinna kujust ja keskkonnast, milles see levib.
Sfäärilised peeglid, läätsed ja neile langevad kiired
Teadmisi teatud kiirte langemisnurkade omadustest kasutatakse sfääriliste peeglite ja õhukeste läätsede kujutiste ehitamisel. Selliste piltide ehitamiseks piisab teadmisest, kuidas käituvad kaks erinevat kiirt nimetatud optiliste seadmetega suhtlemisel. Nende kiirte ristumiskoht määrab pildipunkti asukoha. Üldjuhul võib alati leida kolm erinevat kiirt, mille kulg on täpselt teada (kolmanda kiirega saab kontrollida konstrueeritud kujutise õigsust). Nende kiirte nimed on allpool.
- Jookseb paralleelselt seadme optilise peateljega. See läbib fookuse pärast peegeldumist või murdumist.
- Kiir, mis läbib seadme fookust. See peegeldab alatimurdunud paralleelselt peateljega.
- Läbi optilise keskpunkti (sfäärilise peegli puhul langeb see kokku sfääri keskpunktiga, objektiivi puhul on see selle sees). Selline kiir ei muuda oma trajektoori.
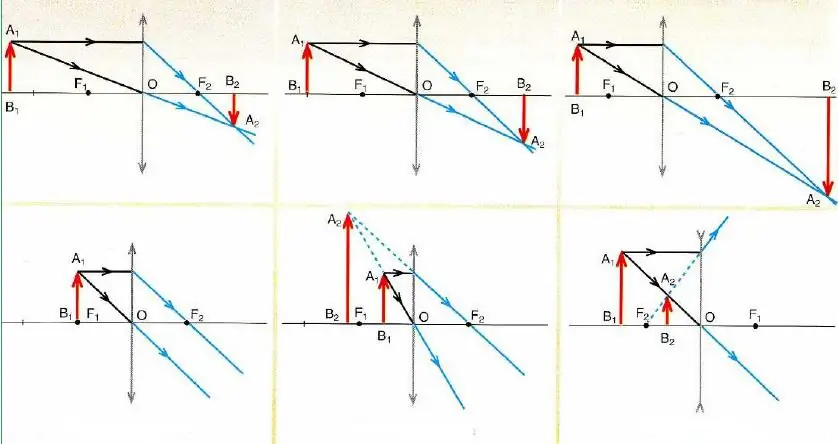
Ül altoodud joonisel on kujutatud kujutiste konstrueerimise skeemid erinevate objektide asukoha ja õhukeste läätsede suhtes.






