Statistikasüsteemides toimuvate protsesside uurimist raskendab osakeste minimaalne suurus ja nende tohutu hulk. Iga osakest eraldi käsitleda on praktiliselt võimatu, seetõttu võetakse kasutusele statistilised suurused: osakeste keskmine kiirus, nende kontsentratsioon, osakeste mass. Valemit, mis iseloomustab süsteemi olekut, võttes arvesse mikroskoopilisi parameetreid, nimetatakse gaaside molekulaarkineetilise teooria (MKT) põhivõrrandiks.
Natuke osakeste keskmise kiiruse kohta
Osakeste kiiruse määramine viidi esm alt läbi eksperimentaalselt. Kooli õppekavast tuntud katse, mille viis läbi Otto Sterni, võimaldas luua aimu osakeste kiirustest. Katse käigus uuriti hõbeda aatomite liikumist pöörlevates silindrites: esm alt paigaldise statsionaarses olekus, seejärel teatud nurkkiirusega pöörlemisel.
Selle tulemusena selgus, et hõbemolekulide kiirus ületab heli kiirust ja on 500 m/s. Fakt on päris huvitav, kuna inimesel on raske tajuda aines olevate osakeste sellist liikumiskiirust.
Ideaalne gaas
Jätkake uurimistTundub võimalik ainult süsteemis, mille parameetreid saab määrata otseste mõõtmiste abil, kasutades füüsilisi instrumente. Kiirust mõõdetakse spidomeetriga, kuid idee spidomeetri kinnitamisest ühele osakesele on absurdne. Otseselt saab mõõta ainult osakeste liikumisega seotud makroskoopilist parameetrit.
Kaaluge gaasirõhku. Rõhk anuma seintele tekib anumas olevate gaasimolekulide mõjul. Aine gaasilise oleku omapäraks on osakeste piisav alt suured vahemaad ja nende väike vastastikmõju. See võimaldab teil selle rõhku otse mõõta.
Mis tahes vastastikku mõjutavate kehade süsteemi iseloomustab potentsiaalne energia ja liikumise kineetiline energia. Pärisgaas on keeruline süsteem. Potentsiaalse energia muutlikkus ei sobi süstematiseerimiseks. Probleemi saab lahendada, võttes kasutusele mudeli, mis kannab gaasi iseloomulikke omadusi, jättes kõrvale interaktsiooni keerukuse.
Ideaalne gaas on aine olek, milles osakeste vastastikmõju on tühine, vastasmõju potentsiaalne energia kipub nulli. Märkimisväärseks võib pidada ainult liikumisenergiat, mis sõltub osakeste kiirusest.
Ideaalne gaasirõhk
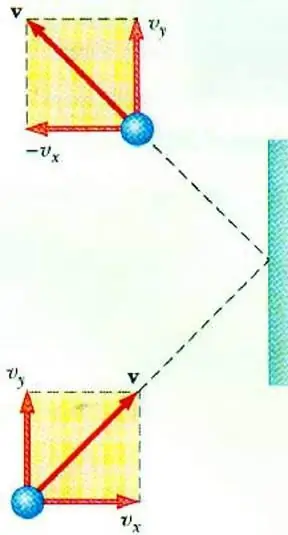
Gaasi rõhu ja selle osakeste kiiruse vahelise seose paljastamine võimaldab ideaalse gaasi MKT põhivõrrandi. Anumas liikuv osake annab seinaga kokkupõrkel sellele impulsi, mille väärtust saab määrata teise seaduse alusel. Newton:
F∆t=2m0vx
Osakese impulsi muutus elastse löögi ajal on seotud selle kiiruse horisontaalkomponendi muutumisega. F on jõud, mis mõjub osakese küljelt seinale lühiajaliselt t; m0 - osakeste mass.
Kõik gaasiosakesed põrkuvad ala S pinnaga aja ∆t jooksul, liikudes pinna suunas kiirusega vx ja paiknevad silindris mahuga Sυ x Δt. Osakeste kontsentratsiooni n korral liiguvad täpselt pooled molekulidest seina poole, teine pool vastupidises suunas.
Võttes arvesse kõigi osakeste kokkupõrget, saame kirjutada Newtoni seaduse alale mõjuva jõu kohta:
F∆t=nm0vx2S∆t
Kuna gaasirõhk on määratletud kui pinnaga risti mõjuva jõu suhe viimase pindalasse, võime kirjutada:
p=F: S=nm0vx2
Saadud seos kui MKT põhivõrrand ei suuda kirjeldada kogu süsteemi, kuna arvestatakse ainult ühte liikumissuunda.
Maxwelli distributsioon
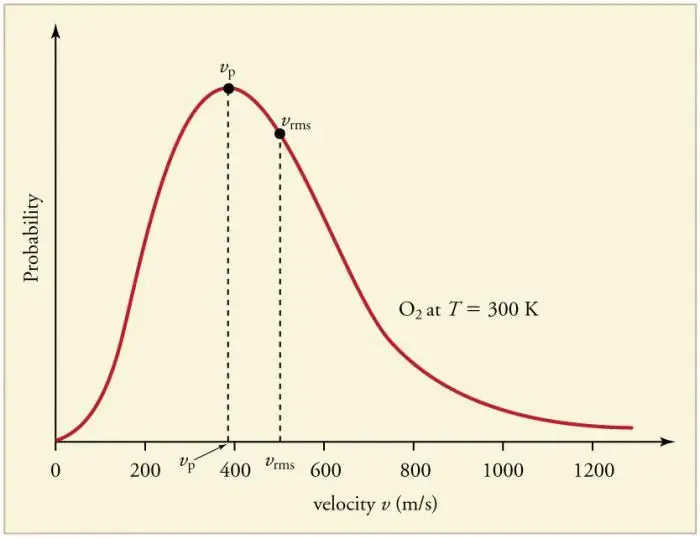
Gaasiosakeste pidevad sagedased kokkupõrked seintega ja üksteisega viivad osakeste teatud statistilise jaotuse kujunemiseni kiiruste (energiate) osas. Kõigi kiirusvektorite suunad osutuvad võrdselt tõenäolisteks. Seda jaotust nimetatakse Maxwelli jaotuseks. Aastal 1860 oli see mustertuletanud J. Maxwell MKT põhjal. Jaotusseaduse peamisi parameetreid nimetatakse kiirusteks: tõenäoline, mis vastab kõvera maksimaalsele väärtusele, ja ruutkeskmine vkv=√‹v2 › - osakeste kiiruse keskmine ruut.
Gaasi temperatuuri tõus vastab kiiruse suurenemisele.
Tuginedes asjaolule, et kõik kiirused on võrdsed ja nende moodulitel on sama väärtus, võime eeldada:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, alates: ‹ vx2›=‹v2›: 3
MKT põhivõrrand, võttes arvesse gaasirõhu keskmist väärtust, on:
p=nm0‹v2›: 3.
See seos on ainulaadne selle poolest, et see määrab seose mikroskoopiliste parameetrite vahel: kiirus, osakeste mass, osakeste kontsentratsioon ja gaasirõhk üldiselt.
Kasutades osakeste kineetilise energia mõistet, saab MKT põhivõrrandi ümber kirjutada erinev alt:
p=2nm0‹v2›: 6=2n‹Ek›: 3
Gaasi rõhk on võrdeline selle osakeste kineetilise energia keskmise väärtusega.
Temperatuur
Huvitaval kombel saab suletud anumas püsiva gaasikoguse korral seostada gaasirõhku ja osakeste liikumisenergia keskmist väärtust. Sel juhul saab rõhku mõõta energia mõõtmise teelosakesed.
Mida teha? Millist väärtust saab võrrelda kineetilise energiaga? Temperatuur osutub selliseks väärtuseks.

Temperatuur on ainete termilise oleku mõõt. Selle mõõtmiseks kasutatakse termomeetrit, mille aluseks on töövedeliku (alkohol, elavhõbe) soojuspaisumine kuumutamisel. Termomeetri skaala luuakse eksperimentaalselt. Tavaliselt asetatakse sellele märgid, mis vastavad töövedeliku asendile mõne konstantses termilises olekus toimuva füüsikalise protsessi käigus (keev vesi, jää sulamine). Erinevatel termomeetritel on erinev skaala. Näiteks Celsius, Fahrenheit.

Universaalne temperatuuriskaala
Gaasitermomeetreid võib pidada huvitavamaks töövedeliku omadustest sõltumatuse poolest. Nende skaala ei sõltu kasutatava gaasi tüübist. Sellises seadmes võib hüpoteetiliselt välja tuua temperatuuri, mille juures gaasirõhk kipub nulli minema. Arvutused näitavad, et see väärtus vastab -273,15 oC. Temperatuuriskaala (absoluutne temperatuuriskaala ehk Kelvini skaala) võeti kasutusele 1848. aastal. Selle skaala põhipunktiks võeti gaasi nullrõhu võimalik temperatuur. Skaala ühikuline segment on võrdne Celsiuse skaala ühikuväärtusega. Gaasiprotsesside uurimisel tundub mugavam MKT põhivõrrand üles kirjutada temperatuuri abil.
Rõhu ja temperatuuri vaheline seos
Empiiriliselt saate seda kontrollidagaasi rõhu proportsionaalsus selle temperatuuriga. Samal ajal leiti, et rõhk on otseselt võrdeline osakeste kontsentratsiooniga:
P=nkT,
kus T on absoluutne temperatuur, k on konstant, mis võrdub 1,38•10-23J/K.
Põhiväärtust, millel on kõigi gaaside jaoks konstantne väärtus, nimetatakse Boltzmanni konstandiks.
Võrreldes rõhu sõltuvust temperatuurist ja MKT gaaside põhivõrrandit, võime kirjutada:
‹Ek›=3kT: 2
Gaasi molekulide liikumise kineetilise energia keskmine väärtus on võrdeline selle temperatuuriga. See tähendab, et temperatuur võib olla osakeste liikumise kineetilise energia mõõt.






