On objekte, mis on võimelised muutma neile langeva elektromagnetilise kiirgusvoo tihedust, st kas suurendama seda ühes punktis kogudes või vähendades seda hajutades. Neid objekte nimetatakse füüsikas läätsedeks. Vaatame seda probleemi lähem alt.
Mis on objektiivid füüsikas?
See mõiste tähendab absoluutselt kõiki objekte, mis on võimelised muutma elektromagnetilise kiirguse levimissuunda. See on läätsede üldine määratlus füüsikas, mis hõlmab optilisi prille, magnet- ja gravitatsiooniläätsi.
Selles artiklis keskendutakse optilistele klaasidele, mis on läbipaistvast materjalist objektid, mis on piiratud kahe pinnaga. Üks neist pindadest peab tingimata olema kumerusega (st olema osa piiratud raadiusega sfäärist), vastasel juhul ei ole objektil omadust muuta valguskiirte levimissuunda.
Läätse põhimõte

Selle lihtsa töö olemusoptiline objekt on päikesekiirte murdumise nähtus. 17. sajandi alguses avaldas kuulus Hollandi füüsik ja astronoom Willebrord Snell van Rooyen murdumisseaduse, mis praegu kannab tema perekonnanime. Selle seaduse sõnastus on järgmine: kui päikesevalgus läbib kahe optiliselt läbipaistva keskkonna liidest, siis valgusvihu ja pinnanormaali vahelise langemisnurga siinuse ja keskkonna murdumisnäitaja korrutis. see levib on konstantne väärtus.

Eelneva selgituseks toome näite: laske valgusel langeda veepinnale, samal ajal kui pinna ja kiire vaheline nurk on θ1. Seejärel valguskiir murdub ja hakkab levima vees juba pinnanormaali suhtes nurga θ2. Vastav alt Snelli seadusele saame: sin(θ1)n1=sin(θ2) n2, kus n1 ja n2 on õhu ja vee murdumisnäitajad, vastav alt. Mis on murdumisnäitaja? See on väärtus, mis näitab, mitu korda on elektromagnetlainete levimiskiirus vaakumis suurem kui optiliselt läbipaistva keskkonna oma, st n=c/v, kus c ja v on valguse kiirused vaakumis ja vaakumis. vastav alt keskmine.
Murdumise ilmnemise füüsika seisneb Fermat' printsiibi elluviimises, mille kohaselt valgus liigub nii, et ületab kauguse ühest ruumipunktist teise kõige lühema ajaga.
Läätsede tüübid

Optilise läätse tüübi füüsikas määrab ainult seda moodustavate pindade kuju. Sellest kujust sõltub neile langeva kiire murdumissuund. Seega, kui pinna kumerus on positiivne (kumer), siis läätsest väljumisel levib valguskiir oma optilisele teljele lähemale (vt allpool). Ja vastupidi, kui pinna kumerus on negatiivne (nõgus), siis optilist klaasi läbides eemaldub kiir oma keskteljest.
Pange veelkord tähele, et mis tahes kumerusega pind murrab kiiri ühtemoodi (vastav alt Stella seadusele), kuid nende normaalidel on optilise telje suhtes erinev kalle, mille tulemuseks on murdunud kiire käitumine.
Kahe kumera pinnaga piiratud läätse nimetatakse koonduvaks läätseks. Omakorda, kui selle moodustavad kaks negatiivse kumerusega pinda, siis nimetatakse seda hajumiseks. Kõik muud tüüpi optilised klaasid on seotud nende pindade kombinatsiooniga, millele on lisatud ka tasapind. Kombineeritud läätse omadus (divergentne või koonduv) sõltub selle pindade raadiuste kogukõverusest.
Läätseelemendid ja kiirte omadused

Läätsede sisseehitamiseks pildifüüsikas peate tutvuma selle objekti elementidega. Need on loetletud allpool:
- Peamine optiline telg ja keskpunkt. Esimesel juhul tähendavad need sirgjoont, mis kulgeb läätsega risti läbi selle optilise keskpunkti. Viimane on omakorda läätse sees asuv punkt, mida läbides kiir ei murdu.
- Fookuskaugus ja fookus - kaugus keskpunkti ja optilise telje punkti vahel, mis kogub kõik selle teljega paralleelselt objektiivile langevad kiired. See määratlus kehtib optiliste klaaside kogumise kohta. Divergentsete läätsede puhul ei koondu punkti mitte kiired ise, vaid nende kujuteldav jätk. Seda punkti nimetatakse põhifookuseks.
- Optiline võimsus. See on fookuskauguse pöördväärtuse nimi, see tähendab D \u003d 1 / f. Seda mõõdetakse dioptrites (dioptrites), see tähendab 1 dioptris.=1 m-1.
Järgmised on objektiivi läbivate kiirte peamised omadused:
- optilist keskpunkti läbiv kiir ei muuda selle liikumissuunda;
- optilise põhiteljega paralleelselt langevad kiired muudavad oma suunda nii, et need läbivad põhifookuse;
- kiired, mis langevad optilisele klaasile mis tahes nurga all, kuid läbivad selle fookust, muudavad oma levimissuunda nii, et need muutuvad paralleelseks optilise põhiteljega.
Füüsikas õhukeste läätsede kiirte ül altoodud omadusi (nagu neid nimetatakse, sest olenemata sellest, mis sfäärid nad on moodustatud ja kui paksud nad on, loevad ainult objekti optilised omadused) nendesse kujutiste koostamiseks..
Pildid optilistes klaasides: kuidas ehitada?
Allpool on joonis, mis kirjeldab kujutiste konstrueerimise skeeme objekti kumer- ja nõgusläätsedes(punane nool) olenev alt selle asukohast.
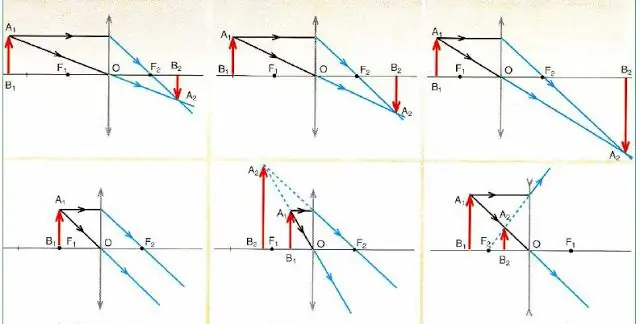
Joonisel kujutatud ahelate analüüsist tulenevad olulised järeldused:
- Iga pilt on üles ehitatud ainult kahele kiirele (läbib keskpunkti ja paralleelselt optilise peateljega).
- Koonduvad läätsed (tähistatud nooltega otstes, mis on suunatud väljapoole) võivad anda nii suurendatud kui ka vähendatud kujutise, mis omakorda võib olla reaalne (päris) või kujuteldav.
- Kui objekt on fookuses, siis objektiiv ei moodusta oma kujutist (vt alumist diagrammi joonisel vasakul).
- Hajutavad optilised klaasid (tähistatud nooltega nende otstes, mis on suunatud sissepoole) annavad alati vähendatud ja virtuaalse pildi olenemata objekti asukohast.
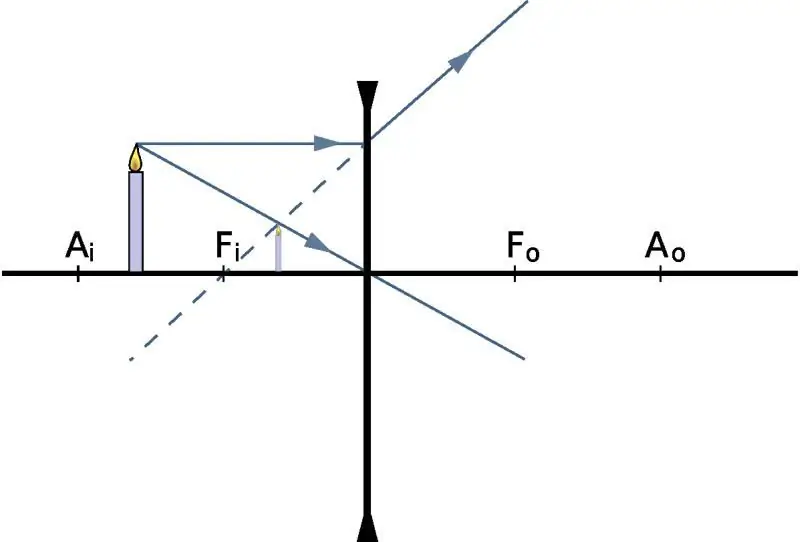
Kujutise kauguse leidmine
Et teha kindlaks, millisel kaugusel pilt ilmub, teades objekti enda asukohta, anname füüsikas objektiivi valemi: 1/f=1/do + 1 /d i, kus do ja di on kaugus objektist ja selle kujutisest optilisest keskpunkt, vastav alt f on põhifookus. Kui me räägime koguvast optilisest klaasist, siis on f-arv positiivne. Ja vastupidi, lahkneva objektiivi korral on f negatiivne.
Kasutame seda valemit ja lahendame lihtsa ülesande: olgu objekt koguva optilise klaasi keskpunktist do=2f kaugusel. Kus tema pilt ilmub?
Ülesande tingimuse põhjal saame: 1/f=1/(2f)+1/di. Alates: 1/di=1/f - 1/(2f)=1/(2f), st di=2 f. Seega kuvatakse pilt objektiivist kahe fookuse kaugusel, kuid teisel pool kui objekt ise (sellele viitab väärtuse di positiivne märk).
Lühike ajalugu
Sõna "objektiiv" etümoloogia on uudishimulik. See pärineb ladinakeelsetest sõnadest lens ja lentis, mis tähendab "lääts", kuna optilised objektid näevad oma kujult välja nagu selle taime vili.
Sfääriliste läbipaistvate kehade murdumisjõud oli teada juba vanadele roomlastele. Selleks kasutasid nad ümmargusi veega täidetud klaasist anumaid. Klaasläätsi ise hakati valmistama alles 13. sajandil Euroopas. Neid kasutati lugemisvahendina (kaasaegsed prillid või suurendusklaas).
Optiliste objektide aktiivne kasutamine teleskoopide ja mikroskoopide valmistamisel pärineb 17. sajandist (selle sajandi alguses leiutas Galileo esimese teleskoobi). Pange tähele, et Stella murdumisseaduse matemaatiline sõnastus, mille teadmata on võimatu soovitud omadustega läätsi valmistada, avaldas Hollandi teadlane sama 17. sajandi alguses.
Muud objektiivid
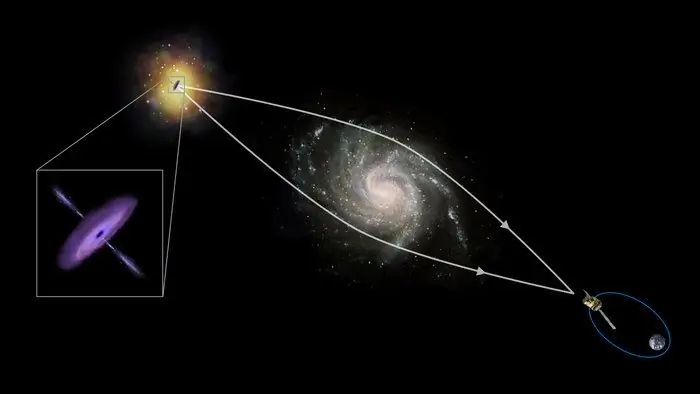
Nagu eespool märgitud, on lisaks optiliselt murduvatele objektidele ka magnetilised ja gravitatsioonilised objektid. Esimeste näideteks on magnetläätsed elektronmikroskoobis, teise ilmekaks näiteks valgusvoo suuna moonutamine,kui see möödub massiivsete kosmosekehade (tähed, planeedid) lähed alt.






