Dünaamiliste juhtimissüsteemide analüüsi üks peamisi ülesandeid on nende stabiilsuse probleemi lahendamine. Nende stabiilsus on juhtimiskontseptsiooni üks olulisemaid omadusi. Süsteem loetakse ebastabiilseks, kui see ei naase oma algsesse asendisse, vaid jätkab võnkumist pärast seda, kui selle sisendis on tehtud mõningaid muudatusi või kui see on soovimatute häirete mõju all.
Põhimõiste määratlus
Süsteemi stabiilsuse kontseptsiooni kohaselt on selle tasakaaluseisund tingitud häirivate tegurite mõju puudumisest. Selles olukorras kipub erinevus määratud ja tegeliku oleku vahel olema null. Stabiilsus on selle võime naasta algsesse tasakaaluolekusse pärast seda, kui selle rikkumiseni viinud häire on lõppenud. Ebastabiilne süsteem häire mõjul eemaldub tasakaaluolekust või võngub, mille amplituud järk-järgulttõuseb.

Stabiilsustingimused
Konstantse ajaga süsteemi stabiilsuse tagamiseks peavad olema täidetud kaks järgmist tingimust:
- Ta loob iga sisendi jaoks piiratud väljundi; kui sisendit pole, peab väljund olema null, olenemata algtingimustest.
- Süsteemi stabiilsust võib nimetada absoluutseks või suhteliseks stabiilsuseks. Esitatud terminit kasutatakse seoses uuringuga, milles võrreldakse teatud koguseid, nende töötingimusi. Stabiilsus on tulemuse loodud lõpptulemus.
Kui süsteemi väljund on lõpmatu, isegi kui sellele on rakendatud piiratud sisend, siis öeldakse, et see on ebastabiilne, st oma olemuselt stabiilne, sellel on piiratud lõpp, kui süsteemile rakendatakse piiratud algust. ise.
Sellisel juhul mõistetakse sisendi all väliskeskkonna mõju süsteemile erinevaid rakenduspunkte. Väljund on tema tegevuse lõpptoode, mis on teisendatud sisendandmete kujul.
Pidevas lineaarses ajasüsteemis saab stabiilsustingimuse kirjutada konkreetse impulssreaktsiooni jaoks.
Kui see on diskreetne, saab stabiilsusindeksi kirjutada ka konkreetse impulssreaktsiooni jaoks.
Ebastabiilse tingimuse korral nii pidevas kui ka piiratud süsteemides on need avaldised lõpmatud.
Stabiilsuse ja häirete tüübid
Staatilise oleku allSüsteemi stabiilsuse all mõistetakse selle võimet tagada algse (või algse lähedase) režiimi taastamine pärast väikest häiringut. Selles kontekstis esitatud kontseptsiooni kohaselt võtavad nad arvesse kõikumist, mis mõjutab selle käitumist, olenemata sellest, kus tõus või langus ilmneb ja milline on nende suurus. Sellest lähtuv alt võimaldavad need esialgsele lähedased režiimid pidada seda lineaarseks.
Süsteemide dünaamiline stabiilsus on viimaste võime taastada algseisund pärast suurt häiret.
Suure kõikumise all mõistetakse sellist liikumist, mille mõju olemus ja sellele vastav käitumine määravad ära eksisteerimise aja, ulatuse ja toimumise koha.
Selle põhjal määratletakse selles vahemikus olev süsteem mittelineaarsena.
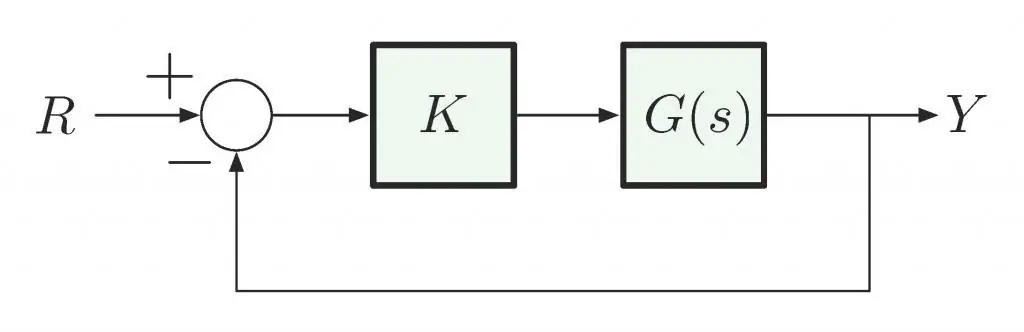
Jätkusuutlikkuse määramise kriteeriumid
Lineaarsüsteemi stabiilsuse põhitingimus ei ole häiringu olemus, vaid selle struktuur. Arvatakse, et see stabiilsus "väikeses" määratakse kindlaks, kui selle piire ei määrata. Stabiilsuse "suures" määravad piirid ja tegelike kõrvalekallete vastavus nendele kehtestatud piiridele.
Süsteemi stabiilsuse määramiseks kasutatakse järgmisi kriteeriume:
- juurkriteerium;
- Stodola kriteerium;
- Hurwitzi kriteerium;
- Nyquisti kriteerium;
- Mihhailovi kriteerium ja teised
Üksikute linkide stabiilsuse määramiseks kasutatakse juurkriteeriumi ja Stodola hindamistehnikatja avatud süsteemid. Hurwitzi kriteerium on algebraline ja võimaldab viivitamata määrata suletud süsteemide stabiilsust. Nyquisti ja Mihhailovi kriteeriumid on sageduslikud. Neid kasutatakse suletud süsteemide stabiilsuse määramiseks nende sageduskarakteristiku põhjal.

Põhikriteerium
See võimaldab teil määrata süsteemi stabiilsuse ülekandefunktsiooni vormi alusel. Selle käitumisomadusi kirjeldatakse iseloomuliku polünoomiga (ülekandefunktsiooni nimetaja). Kui võrdsustame nimetaja nulliga, võimaldavad saadud võrrandi juured määrata stabiilsuse astme.
Selle kriteeriumi järgi on lineaarsüsteem stabiilne, kui kõik võrrandi juured on vasakul pooltasandil. Kui vähem alt üks neist asub stabiilsuspiiril, on see ka piiril. Kui vähem alt üks neist on paremal pooltasandil, võib süsteemi pidada ebastabiilseks.
Stodola kriteerium
See tuleneb juurmääratlusest. Stodola kriteeriumi kohaselt võib lineaarset süsteemi pidada stabiilseks, kui kõik polünoomi koefitsiendid on positiivsed.
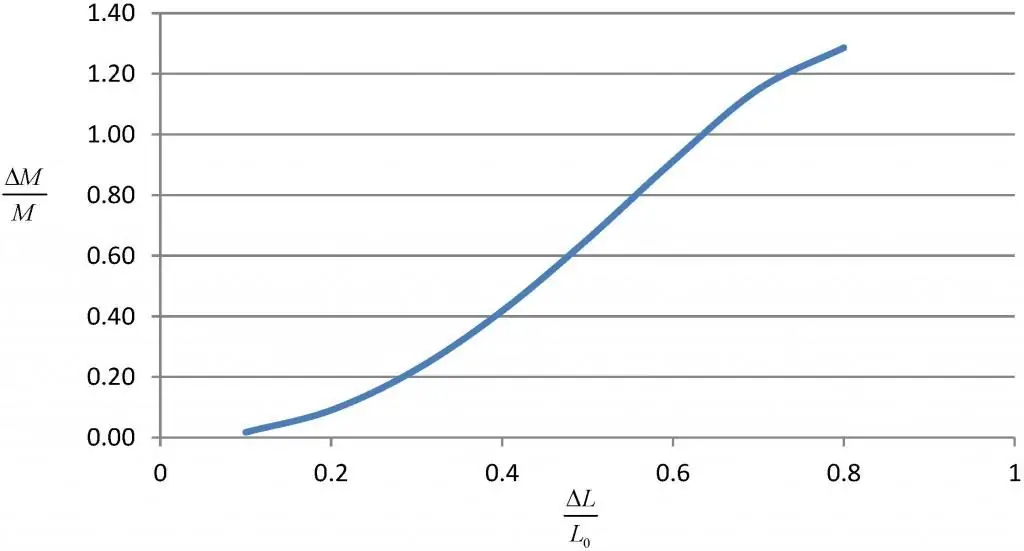
Hurwitzi kriteerium
Seda kriteeriumi kasutatakse suletud süsteemi iseloomuliku polünoomi jaoks. Selle tehnika kohaselt on stabiilsuse piisav tingimus asjaolu, et maatriksi determinandi ja kõigi põhidiagonaalmooloride väärtus on suurem kui null. Kui vähem alt üks neist on võrdnenull, peetakse seda stabiilsuse piiril. Kui on vähem alt üks negatiivne determinant, tuleks seda pidada ebastabiilseks.
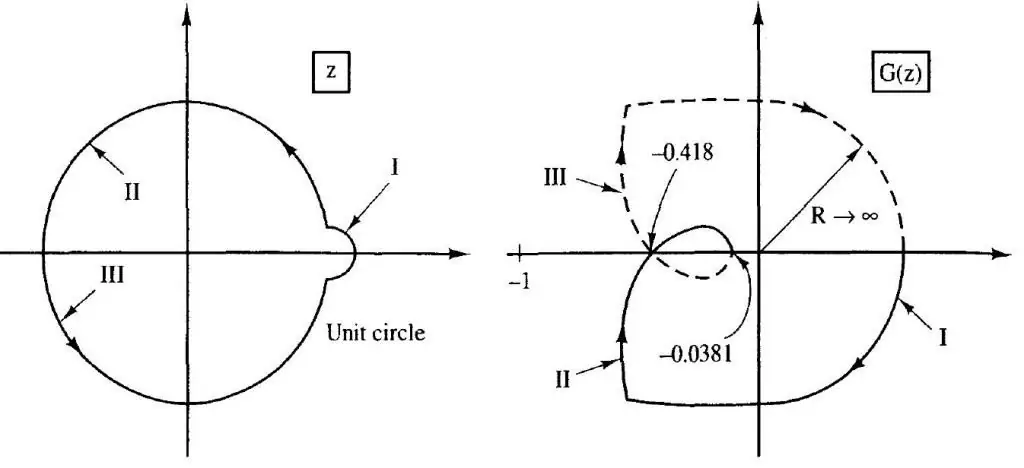
Nyquisti kriteerium
Selle tehnika aluseks on kõvera konstrueerimine, mis ühendab ülekandefunktsiooni kuvava muutuja vektori otsad. Kriteeriumi sõnastus on järgmine: suletud süsteemi peetakse stabiilseks, kui funktsioonikõver ei hõlma komplekstasandil punkti koordinaatidega (-1, j0).
Finantskindluse süsteem
Finantsvastupidavus on seisund, milles süsteem, st peamised turud ja institutsioonid, on vastupidav majandusšokkidele ning on valmis sujuv alt täitma oma põhifunktsioone, nagu rahavoogude vahendamine, riskijuhtimine ja maksekorraldus.
Tõlke pakkumise vastastikusest sõltuvussuhtest (nii vertikaalselt kui ka horisontaalselt) peab analüüs hõlmama kogu finantsvahendussüsteemi. Ehk siis lisaks pangandussektorile on vaja analüüsida ka mittepanganduslikke asutusi, kes ühel või teisel kujul vahendamisega tegelevad. Nende hulka kuuluvad mitut tüüpi institutsioonid, sealhulgas maaklerfirmad, investeerimisfondid, kindlustusandjad ja muud (erinevad) üksused. Finantsstabiilsuse süsteemi analüüsimisel uuritakse, mil määral suudab kogu struktuur välistele ja sisemistele šokkidele vastu pidada. Muidugi ei too alati kriise kaasa šokid, vaid ebastabiilne finantskeskkond isevõib iseenesest takistada majanduse tervet arengut.
Erinevad teooriad toovad välja finantsebastabiilsuse põhjused. Nende asjakohasus võib varieeruda olenev alt perioodist ja analüüsiga hõlmatud riikidest. Kogu finantssüsteemi mõjutavatest probleemsetest teguritest on kirjanduses tavaliselt välja toodud järgmised:
- finantssektori kiire liberaliseerimine;
- ebaadekvaatne majanduspoliitika;
- Sihita vahetuskursi mehhanism;
- ressursside ebaefektiivne jaotamine;
- nõrk järelevalve;
- Ebapiisav raamatupidamise ja auditeerimise regulatsioon.
Võimalikud põhjused ilmnevad mitte ainult kollektiivselt, vaid ka üksikult või juhuslikus kombinatsioonis, seega on finantsstabiilsuse analüüs äärmiselt keeruline ülesanne. Keskendumine üksikutele majandusharudele moonutab üldpilti, mistõttu tuleb finantsstabiilsuse uurimisel käsitleda küsimusi nende keerukuses.

Ettevõtte süsteemi stabiilsuse analüüsiprotsess toimub mitmes etapis.
Esialgu hinnatakse ja analüüsitakse finantsstabiilsuse absoluutseid ja suhtelisi näitajaid. Teises etapis jaotatakse tegurid vastav alt nende olulisusele, nende mõju hinnatakse kvalitatiivselt ja kvantitatiivselt.
Ettevõtete finantstugevuse suhtarvud
Ettevõtte finantsseisund, selle stabiilsus sõltub suuresti kapitaliallikate optimaalsest struktuurist ehk võla ja omavahendite suhtest, optimaalsestettevõtte varade struktuurist ja ennekõike põhi- ja käibevara vahekorrast, samuti ettevõtte rahaliste vahendite ja kohustuste jäägist.
Seetõttu on oluline uurida riskikapitali allikate struktuuri ning hinnata finantsstabiilsuse ja riski astet. Sel eesmärgil kasutatakse süsteemi stabiilsuse koefitsiente:
- autonoomia (iseseisvuse) koefitsient - kapitali osakaal bilansis;
- sõltuvuskordaja - laenukapitali osakaal bilansis;
- lühiajalise võla suhe - lühiajaliste finantskohustuste suhe bilanssi;
- finantsstabiilsuse suhe (pikaajaline finantssõltumatus) - kapitali ja pikaajalise võla suhe bilanssi;
- võlgade kattekordaja (maksevõime suhe) - kapitali ja võla suhe;
- finantsvõimenduse määr (finantsriski suhe) - võla ja kapitali suhe.

Mida kõrgem on selliste näitajate tase nagu autonoomia, finantsstabiilsus, laenukapitali katvus, seda madalam on teise koefitsientide rühma tase (sõltuvus, jooksevvõlg, pikaajalised kohustused investorite ees) ja vastav alt ettevõtte finantsseisundi stabiilsus. Finantsvõimendust nimetatakse ka finantsvõimenduseks.






