Füüsikas uuritakse paralleel- ja jadaühenduse teemat ning see võib olla mitte ainult juhtide, vaid ka kondensaatorite puhul. Siinkohal on oluline mitte sattuda segadusse selle üle, kuidas igaüks neist diagrammil välja näeb. Ja alles siis rakendage konkreetseid valemeid. Muide, peate need peast meeles pidama.
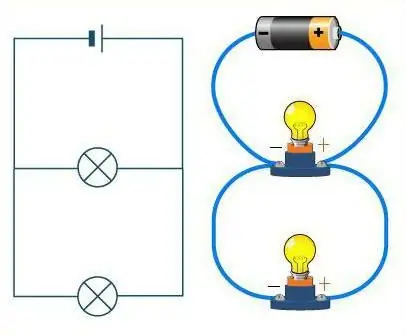
Kuidas neil kahel ühendil vahet teha?
Vaadake diagrammi tähelepanelikult. Kui juhtmed on kujutatud maanteena, mängivad sellel olevad autod takistite rolli. Ilma hargnemata sirgel teel sõidavad autod üksteise järel, ketis. Samasugune näeb välja ka juhtmete jadaühendus. Teel võib sel juhul olla piiramatu arv pöördeid, kuid mitte ühtegi ristmikku. Olenemata sellest, kuidas teed (juhtmed) liiguvad, asuvad masinad (takistid) alati üksteise järel, ühes ahelas.
Asi on hoopis teine, kui mõelda paralleelühendusele. Siis saab takisteid stardis sportlastega võrrelda. Nemad onigaüks seisab oma rajal, kuid neil on sama liikumissuund ja finišijoon on samas kohas. Samamoodi takistid - igaühel neist on oma juhe, aga kõik on mingil hetkel ühendatud.
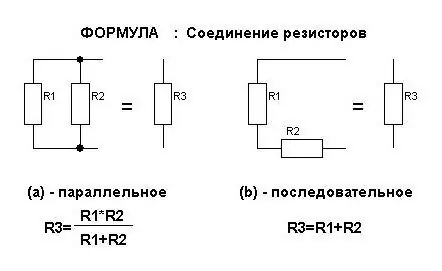
Praegu tugevuse valemid
Sellest tuleb alati juttu teemas "Elekter". Paralleel- ja jadaühendused mõjutavad takistite voolutugevust erineval viisil. Nende jaoks on tuletatud valemid, mida saab meelde jätta. Kuid piisab, kui meeles pidada nendesse panustatud tähendust.
Seega on juhtide jadaühenduses olev vool alati sama. See tähendab, et igaühes neist ei erine voolutugevuse väärtus. Saate tuua analoogia, kui võrrelda traati toruga. Selles voolab vesi alati ühtemoodi. Ja kõik takistused selle teel pühitakse minema sama jõuga. Sama vooluga. Seetõttu näeb takistite jadaühendusega vooluahela koguvoolu valem välja järgmine:
I gen=I 1=I 2
Siin tähistab täht I voolu tugevust. See on levinud märge, nii et peate seda meeles pidama.
Rööpühenduses olev vool ei ole enam konstantne väärtus. Sama analoogiaga toruga selgub, et kui peatorul on haru, jagatakse vesi kaheks vooluks. Sama nähtust täheldatakse vooluga, kui selle teele ilmub juhtmete hargnemine. Koguvoolutugevuse valem, kui juhid on paralleelselt ühendatud:
I gen=I 1 + I 2
Kui hargnemine koosneb juhtmetest, misrohkem kui kaks, siis on ül altoodud valemis sama arvu võrra rohkem termineid.
Stressivalemid
Kui mõeldakse vooluringile, milles juhid on ühendatud järjestikku, määratakse pinge kogu sektsioonis iga konkreetse takisti väärtuste summaga. Seda olukorda saate võrrelda plaatidega. Ühel on lihtne ühte neist käes hoida, teist saab ta ka lähed alt võtta, kuid vaevaliselt. Üks inimene ei suuda enam kolme taldrikut kõrvuti hoida, vaja läheb teise abi. Jne. Inimeste jõupingutused lähevad kokku.
Juhtide jadaühendusega vooluringi lõigu kogupinge valem näeb välja järgmine:
U gen=U 1 + U 2, kus U on kasutusele võetud tähistus elektripinge jaoks.
Tekib teine olukord, kui mõeldakse takistite paralleelühendusele. Kui taldrikud on üksteise peale laotud, saab neid ikka üks inimene hoida. Nii et te ei pea midagi lisama. Sama analoogiat täheldatakse ka siis, kui juhtmed on paralleelselt ühendatud. Kõigil neist on pinge sama ja võrdne sellega, mis on kõigil korraga. Kogupinge valem on:
U gen=U 1=U 2
Elektritakistuse valemid
Sa ei saa neid enam pähe õppida, vaid tead Ohmi seaduse valemit ja tuleta sellest soovitud. Sellest seadusest tuleneb, etpinge on võrdne voolu ja takistuse korrutisega. See tähendab, U=IR, kus R on takistus.
Siis sõltub valem, millega peate töötama, sellest, kuidas juhid on ühendatud:
- seerias, nii et vajate pinge võrdsust - IgenRkokku=I1R1 + I2R2;
- paralleelselt on vaja kasutada voolutugevuse valemit - Ukokku / Rkokku=U 1/ R1 + U2 / R2 .
Järgnevad lihtsad teisendused, mis põhinevad asjaolul, et esimeses võrdsuses on kõik voolud sama väärtusega ja teises - pinged on võrdsed. Nii et neid saab lühendada. See tähendab, et saadakse järgmised avaldised:
- R gen=R 1 + R 2 (juhtide jadaühenduseks)
- 1 / R gen=1 / R 1 + 1 / R 2(kui ühendatud paralleelselt).
Kui võrku ühendatud takistite arv suureneb, muutub nendes avaldistes terminite arv.
Tasub tähele panna, et juhtide paralleel- ja jadaühendusel on kogutakistusele erinev mõju. Esimene neist vähendab vooluringi sektsiooni takistust. Pealegi osutub see väiksemaks kui kasutatud takistitest väikseim. Jadaühendamisel on kõik loogiline: väärtused liidetakse, nii et koguarv on alati suurim.
Töövool
Eelmised kolm suurust moodustavad vooluahela juhtide paralleelühenduse ja järjestikuse paigutuse seadused. Seetõttu on nende tundmine hädavajalik. Töö ja jõu osas peate lihts alt meeles pidama põhivalemit. See on kirjutatud järgmiselt: A \u003d IUt, kus A on voolu töö, t on selle voolu läbimise aeg.
Selleks, et määrata kogu töö jadaühendusega, peate asendama algses avaldises oleva pinge. Saate võrdsuse: A \u003d I(U 1 + U 2)t, avades sulud, milles selgub, et kogu jaotise töö on võrdne nende summaga iga konkreetse praeguse tarbija kohta.
Arutluskäik jätkub samamoodi, kui vaadeldakse paralleelühenduse skeemi. Ainult praegune tugevus peaks asendama. Kuid tulemus on sama: A=A 1 + A 2.
Praegune võimsus
Ahela sektsiooni võimsuse valemi (tähis "P") tuletamisel peate taas kasutama ühte valemit: P \u003d UI. Pärast sellist arutluskäiku selgub, et paralleel- ja jadaühendused on kirjeldatakse sellise võimsuse valemiga: P \u003d P1 + P 2.
See tähendab, et olenemata sellest, kuidas skeemid on koostatud, on koguvõimsus töös osalejate summa. See seletab asjaolu, et korterivõrku on võimatu korraga kaasata palju võimsaid seadmeid. Ta lihts alt ei talu koormust.
Kuidas mõjutab juhtmete ühendamine aastavahetuse vaniku remonti?
Kohe pärast ühe pirni läbipõlemist selgub, kuidas need ühendati. Kelljadaühendus, ükski neist ei sütti. See on tingitud asjaolust, et kasutuskõlbmatuks muutunud lamp tekitab vooluringis katkestuse. Seetõttu peate kõike kontrollima, et teha kindlaks, milline neist on läbi põlenud, ja asendage see - ja vanik hakkab tööle.
Kui see kasutab paralleelühendust, ei lakka see töötamast, kui üks pirnidest üles ütleb. Lõppude lõpuks ei katke kett täielikult, vaid ainult üks paralleelne osa. Sellise vaniku parandamiseks ei pea te kontrollima kõiki vooluringi elemente, vaid ainult neid, mis ei helenda.
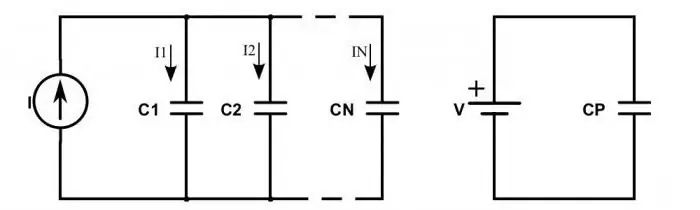
Mis juhtub vooluringiga, kui takistite asemel on kaasas kondensaatorid?
Kui need on järjestikku ühendatud, täheldatakse järgmist olukorda: toiteallika plusside laengud tulevad ainult äärmuslike kondensaatorite välisplaatidele. Need, kes on vahepeal, edastavad selle laengu lihts alt mööda ketti. See seletab asjaolu, et kõigil plaatidel on samad laengud, kuid erinevate märkidega. Seetõttu saab iga järjestikku ühendatud kondensaatori elektrilaengu kirjutada järgmiselt:
q gen =q 1=q 2.
Iga kondensaatori pinge määramiseks peate teadma valemit: U=q / C. Selles on C kondensaatori mahtuvus.
Kogupinge järgib sama seadust nagu takistitel. Seega, asendades pinge mahtuvuse valemis summaga, saame, et seadmete kogumahtuvus tuleb arvutada järgmise valemi abil:
C=q / (U 1 + U2).
Seda valemit saate lihtsustada, pöörates murde ümber ja asendades pinge ja laengu suhte mahtuvusega. Selgub järgmine võrdsus: 1 / С=1 / С 1 + 1 / С 2.
Kui kondensaatorid on paralleelselt ühendatud, tundub olukord mõnevõrra erinev. Seejärel määratakse kogulaeng kõigi seadmete plaatidele kogunevate laengute summaga. Ja pinge väärtus määratakse ikka üldiste seaduste järgi. Seetõttu on paralleelselt ühendatud kondensaatorite kogumahtuvuse valem:
С=(q 1 + q 2) / U.
See tähendab, et seda väärtust peetakse kõigi ühenduses kasutatud seadmete summaks:
S=S 1 + S 2.
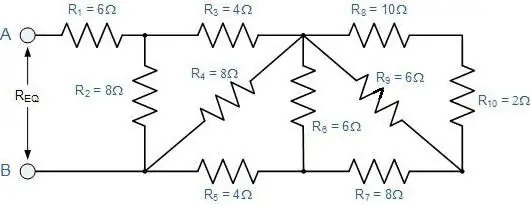
Kuidas määrata juhtide suvalise ühendamise kogutakistust?
See tähendab, et järjestikused lõigud asendavad paralleelseid ja vastupidi. Nende jaoks kehtivad siiani kõik kirjeldatud seadused. Ainult teil on vaja neid rakendada etapiviisiliselt.
Esiteks, see peaks skeemi vaimselt laiendama. Kui seda on raske ette kujutada, siis peate joonistama, mis juhtub. Seletus saab selgemaks, kui käsitleme seda konkreetse näitega (vt joonist).
Joonistamist on mugav alustada punktidest B ja C. Need tuleb asetada üksteisest ja lehe servadest teatud kaugusele. Vasakul läheneb üks juhe punktile B ja kaks on juba suunatud paremale. Punktil B on aga kaks haru vasakul ja üks juhe pärast seda.
Nüüd peate täitma nendevahelise ruumipunktid. Ülemise juhtme äärde tuleks asetada kolm takistit koefitsientidega 2, 3 ja 4, alt läheb indeksiga 5. Esimesed kolm on ühendatud järjestikku. Viienda takistiga on need paralleelsed.
Ülejäänud kaks takistit (esimene ja kuues) on ühendatud BV vaadeldava osaga järjestikku. Seetõttu saab joonist lihts alt täiendada kahe ristkülikuga valitud punktide mõlemal küljel. Jääb üle rakendada takistuse arvutamiseks valemeid:
- kõigepe alt see, mis on antud jadaühenduse jaoks;
- siis paralleelseks;
- ja uuesti järjest.
Nii saate juurutada mis tahes, isegi väga keeruka skeemi.
Juhtmete jadaühenduse probleem
Seisukord. Kaks lampi ja takisti on ühendatud ahelasse üksteise taha. Kogupinge on 110 V ja vool 12 A. Mis on takisti väärtus, kui iga lambi nimipinge on 40 V?
Otsus. Kuna kaalutakse jadaühendust, on selle seaduste valemid teada. Peate neid lihts alt õigesti rakendama. Alustage takisti pinge väärtuse leidmisega. Selleks peate kogusummast lahutama ühe lambi kahekordse pinge. Selgub, et 30 V.
Nüüd, kui on teada kaks suurust, U ja I (neist teine on tingimuses antud, kuna koguvool on võrdne iga seeriatarbija vooluga), saame takisti takistuse arvutada kasutades Ohmi seadus. Selgub, et see on 2,5 oomi.
Vastus. Takisti takistus on 2,5 oomi.
Ülesannekondensaatorite, paralleel- ja jadaühendamiseks
Seisukord. Seal on kolm kondensaatorit võimsusega 20, 25 ja 30 mikrofaradi. Määrake nende kogumahtuvus, kui need on ühendatud järjestikku ja paralleelselt.
Otsus. Lihtsam on alustada paralleelühendusega. Sellises olukorras tuleb kõik kolm väärtust lihts alt lisada. Seega on kogumahtuvus 75uF.
Kui need kondensaatorid on järjestikku ühendatud, on arvutused mõnevõrra keerulisemad. Lõppude lõpuks peate esm alt leidma nende võimsuste ühtsuse suhte ja seejärel need üksteisega liitma. Selgub, et ühik jagatud koguvõimsusega on 37/300. Siis on soovitud väärtus ligikaudu 8 mikrofaradi.
Vastus. Jadaühenduse kogumahtuvus on 8 uF, paralleelselt - 75 uF.




